La Crittografia Post-Quantum (PQC): una soluzione classica alla minaccia quantistica
Introduzione
La crittografia a chiave pubblica (o asimmetrica) è una delle basi sulle quali poggiano tutti i protocolli di comunicazione che, a partire da un canale insicuro, devono raggiungere molteplici proprietà di sicurezza, come ad esempio segretezza o integrità dell’informazione. A quest’area afferiscono diverse tecniche crittografiche, tra cui gli algoritmi di negoziazione delle chiavi e quelli di firma digitale. Questi ricoprono un posto di rilievo, sia per maturità tecnologica che per adozione in protocolli ampiamente diffusi come TLS, IPsec o WireGuard.
Le tecniche crittografiche asimmetriche basano la propria sicurezza sulla presunta intrattabilità di alcuni problemi matematici, ovvero problemi per cui non è noto alcun algoritmo in grado di risalire alla soluzione in maniera computazionalmente efficiente e, pur appoggiandosi ai più potenti sistemi di calcolo oggi a disposizione, un’eventuale risoluzione richiederebbe tempi impraticabili (migliaia di anni). Alcuni esempi sono il problema della fattorizzazione dei numeri interi e il problema del logaritmo discreto, il primo alla base del crittosistema RSA e il secondo del protocollo Diffie-Hellman.
Questi due problemi costituiscono la totalità di quelli impiegati negli algoritmi asimmetrici standardizzati e nonostante siano resistiti a decenni di crittoanalisi, gli sviluppi recenti nel campo della computazione quantistica potrebbero rappresentare una minaccia concreta. In particolare, qualora un opportuno computer quantistico venisse realizzato l’algoritmo quantistico di Shor (1994) riuscirebbe a rompere i due problemi sopra citati in tempi ragionevoli, impattando la sicurezza di tutta la crittografia a chiave pubblica oggi in uso.
Nonostante l’implementabilità nel medio-lungo termine dell’algoritmo di Shor rimanga dubbia viste le importanti sfide tecnologiche poste dalla realizzazione di elaboratori quantistici, la National Security Agency (NSA) americana ha manifestato pubblicamente nel 2015 la necessità di un piano di transizione ad algoritmi crittografici quantum-resistant, cioè resistenti agli attacchi di un computer quantistico.
Infatti, sebbene sia ancora complesso esprimere una valutazione precisa circa l’orizzonte temporale in cui i computer quantistici potrebbero costituire una minaccia concreta alla crittografia a chiave pubblica, è auspicabile che un processo di transizione venga concluso quanto prima, in modo da minimizzare i rischi legati alla sicurezza a lungo termine dell’informazione. Infatti, già oggi un attaccante potrebbe adottare strategie del tipo “store now, decrypt later”, intercettando e memorizzando il traffico cifrato con lo scopo di utilizzare in futuro un computer quantistico per la decifratura dei dati. Al tempo stesso, il periodo di transizione a nuove tecniche crittografiche non è trascurabile e in questo caso è necessario completarlo anticipando la realizzazione di un opportuno computer quantistico, pena l’esposizione insicura delle informazioni.
Le principali tecniche quantum-resistant affrontate in questo scenario sono la Quantum Key Distribution (QKD) e la Post-Quantum Cryptography (PQC). La prima è una risposta fisica e infrastrutturale al problema dello scambio chiave su canale insicuro: utilizzando i principi della fisica quantistica è possibile stabilire un protocollo con sicurezza incondizionata che permetta a due parti di negoziare una chiave crittografica con cui proteggere successivamente le loro comunicazioni. Questa tecnica non è basata sull’assunzione che alcuni problemi matematici siano intrattabili ma affonda le sue radici nelle leggi fisiche.
La Post-Quantum Cryptography (PQC) è, invece, una risposta classica all’avvento del calcolo quantistico. La PQC si occupa, infatti, del design di schemi crittografici a chiave pubblica implementabili su elaboratori classici e resistenti anche ad attacchi di tipo quantistico. Di conseguenza, le tecniche crittografiche post-quantum basano la propria sicurezza su problemi matematici per cui non sono noti algoritmi risolutivi efficienti, indipendentemente dalla loro natura classica o quantistica. Ad esempio, RSA e Diffie-Hellman, basandosi su problemi risolvibili con l’algoritmo quantistico di Shor, non possono essere considerati post-quantum.
Oggetto del presente articolo sarà proprio un’introduzione alla PQC, argomento che sarà poi ulteriormente investigato in contributi successivi maggiormente focalizzati su alcuni aspetti più tecnici della materia.
La competizione del NIST
Lo sviluppo della crittografia post-quantum ha ricevuto un notevole impulso nel 2017, quando il National Institute of Standards and Technology (NIST) americano ha avviato un processo di standardizzazione per definire ed analizzare nuovi schemi nell’ambito della crittografia a chiave pubblica che siano quantum-resistant. In particolare, le due categorie di tecniche crittografiche oggetto della standardizzazione sono Key-Encapsulation Mechanisms (KEMs) e firme digitali.
Per quanto riguarda le firme digitali, l’adozione di alternative post-quantum andrebbe ad inserirsi in modo trasparente nei protocolli esistenti, senza modificarne la struttura ad alto livello. Un discorso leggermente diverso va fatto per i KEMs: allo stato dell’arte attuale non è presente un’alternativa post-quantum pratica al protocollo di Diffie-Hellman che permette lo scambio “non-interattivo” di chiavi, pertanto per la negoziazione della chiave si utilizza una tecnica, detta di incapsulamento, legata alla cifratura a chiave pubblica, talvolta causando la variazione della struttura logica alla base degli attuali protocolli.
La competizione del NIST, ha raccolto numerose proposte per un totale di 64, di cui 45 KEMs e 19 firme digitali. In seguito ai primi tre round di studio e scrematura dei candidati, il 5 luglio 2022 sono stati comunicati i vincitori della prima fase di standardizzazione, 1 KEM e 3 firme digitali, e i candidati soggetto di ulteriori valutazioni in un quarto round, 4 KEM. I problemi matematici considerati dai candidati del terzo round sono stati di varia natura, basandosi su strutture matematiche quali reticoli algebrici, codici lineari, sistemi di equazioni multivariate, isogenie di curve ellittiche supersingolari e primitive simmetriche.
Si tratta di problemi matematici a priori indipendenti tra loro per cui le eventuali criticità di uno non implicano problemi di sicurezza per gli altri. Le famiglie di problemi sono riportate in forma sintetica nella tabella sottostante:
| Famiglia di problemi PQC | Esempi KEMs | Esempi Firme Digitali |
| Reticoli | Kyber, NTRU, Saber | Dilithium, Falcon |
| Codici | Classic McEliece, BIKE, HQC | |
| Sistemi multivariati | Rainbow | |
| Primitive simmetriche | SPHINCS+, Picnic | |
| Isogenie di curve ellittiche | SIKE |
In grassetto vincitori del III round, in corsivo candidati IV round
Nonostante la chiusura della competizione fosse prevista per marzo 2022, l’esito finale è stato reso pubblico con qualche mese di ritardo a causa di alcune complicazioni burocratiche come dichiarato dal NIST. Da un punto di vista tecnico, è rilevante riportare anche che all’inizio di quest’anno è stato realizzato un attacco allo schema di firma digitale Rainbow, uno dei finalisti del terzo round, basato su crittografia multivariata.
Questo ha portato ad una maggiore prudenza da parte del NIST e ha avvalorato ulteriormente l’intenzione, già precedentemente espressa per la scarsa diversità dei candidati rimanenti, di riaprire la competizione nella categoria delle firme digitali. Infatti, due dei tre algoritmi standardizzati per questa categoria sono basati su reticoli, dando quindi poca varietà ai possibili schemi da adottare. Da un punto di vista della sicurezza e considerata l’innovatività delle soluzioni proposte, è bene avere schemi con assunzioni crittografiche più varie possibili.
Le sfide della transizione
Il fine ultimo nello sviluppo della PQC è la sostituzione degli algoritmi classici all’interno dei protocolli di comunicazione sicura, minimizzando l’impatto della transizione a soluzioni quantum-resistant, potenzialmente limitando la necessità di intervenire a livelli di protocollo, rete e sistema. D’altra parte, è importante osservare che il processo di transizione dell’attuale infrastruttura di crittografia a chiave pubblica ai nuovi standard non potrà limitarsi ad una semplice sostituzione degli algoritmi e che le sfide introdotte dalla minaccia quantistica riguarderanno necessariamente il funzionamento dei vari livelli che contribuiscono alla realizzazione dell’infrastruttura di sicurezza.
Nonostante le comuni funzionalità ed interfacce, gli algoritmi PQC risultano estremamente eterogenei, con differenze in termini di dimensioni delle chiavi, di firme e cifrati, di requisiti computazionali e di comunicazione. Anche per questa ragione, il NIST ha affermato che la competizione porterà molto probabilmente alla standardizzazione di più di una proposta, in modo da coprire un’ampia varietà di requisiti e casi d’uso.
Maggiori requisiti in termini di risorse di calcolo rappresentano un problema centrale nell’adozione di uno schema crittografico da parte dell’industria. Semplificando, un maggiore costo computazionale si traduce in maggiori costi in termini di tempo ed energia consumata. Questi costi sono direttamente misurabili e rappresentano un limite talvolta insormontabile per dispositivi con elevati requisiti di traffico o con limitate risorse (es. IoT, embedded). Pertanto, numerosi sforzi sono rivolti allo sviluppo di ottimizzazioni a livello di algoritmi, implementazioni software e hardware, per soddisfare i requisiti dei protocolli di rete delle connessioni sempre più veloci.
Un problema all’apparenza meno pressante ma con altrettante implicazioni in scenari reali riguarda l’incremento sistematico delle dimensioni di chiavi e firme nelle proposte PQC (vedi i grafici riportati sotto). Valutare correttamente l’impatto in questo caso risulta più arduo e ci aspettiamo possa riguardare soprattutto il livello di rete. Ad esempio, una maggiore dimensione delle chiavi si rifletterà probabilmente sulla trasmissione dei pacchetti IP durante l’esecuzione di protocolli di comunicazione sicura, introducendo una maggiore latenza e maggiori requisiti in termini di banda. Talvolta potrebbero manifestarsi degli effetti a catena causati dai dispositivi di rete intermedi (es. router, firewall) non più compatibili con le dimensioni dei nuovi standard, andando ad aumentare la frammentazione e la perdita dei pacchetti.

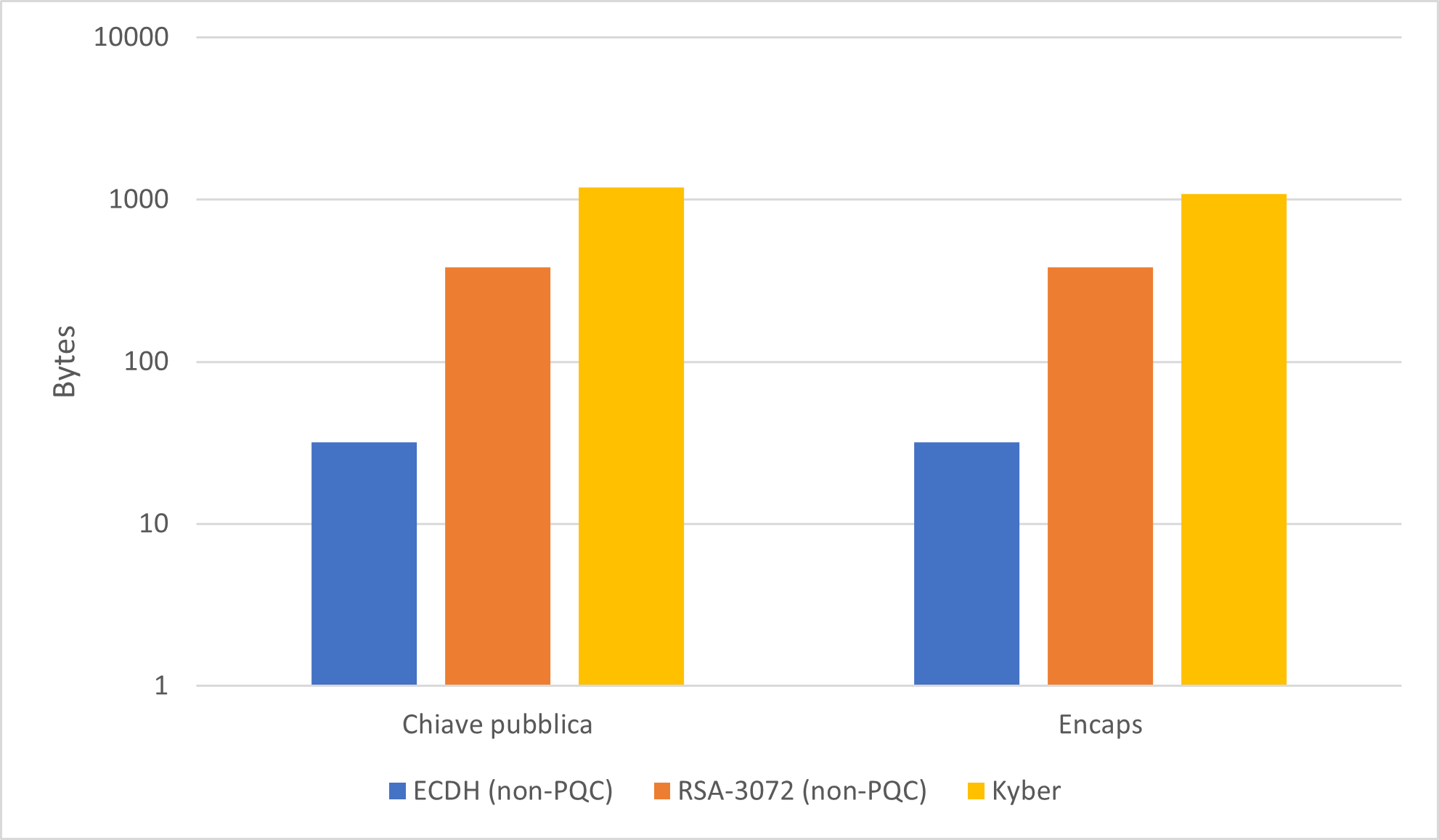

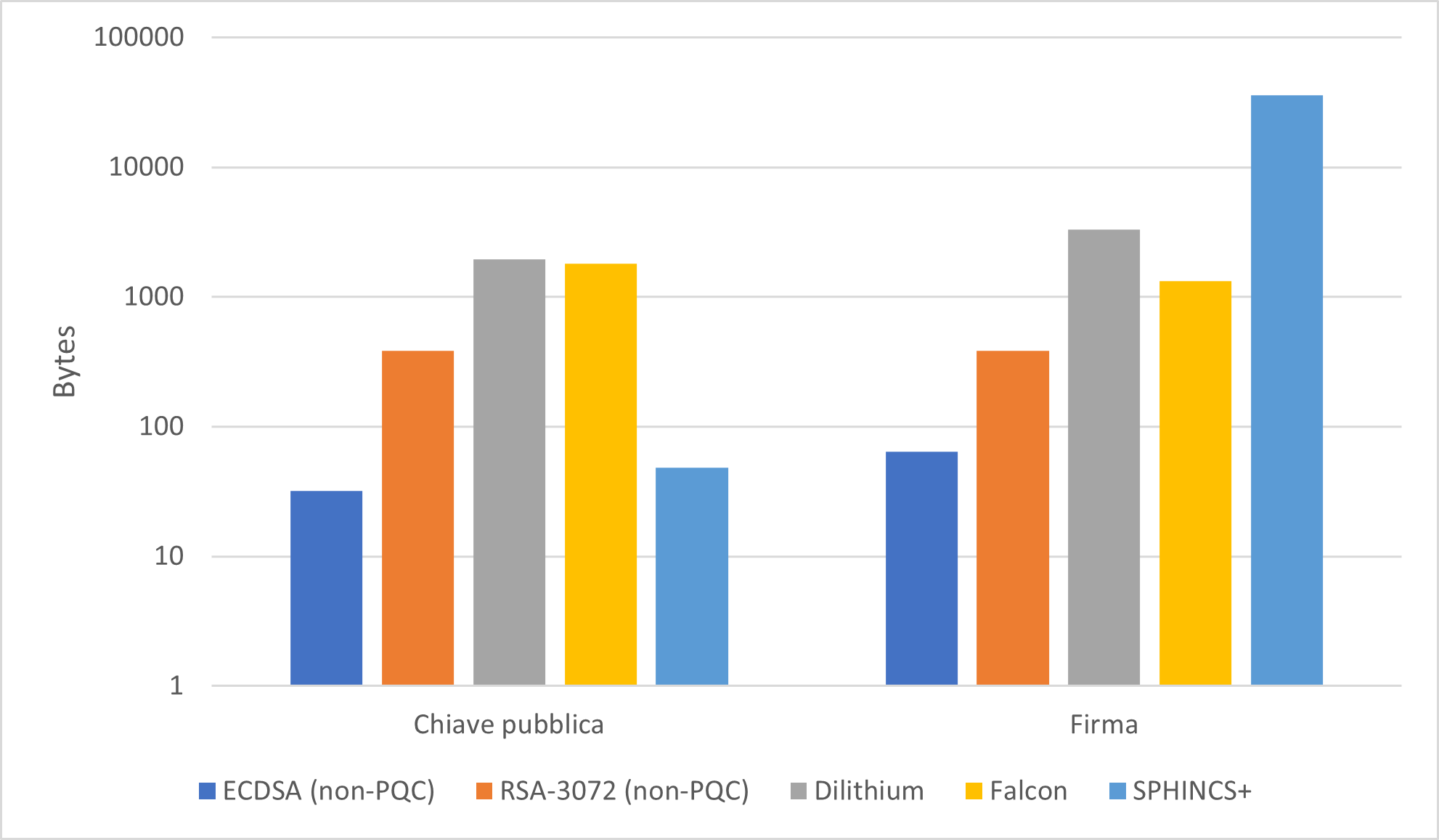
La transizione ad algoritmi post-quantum rappresenta una sfida complessa ma estremamente attuale, che richiede un lavoro su più livelli e l’impegno congiunto da parte del mondo della ricerca e dell’industria. Il dominio della sicurezza è in continua evoluzione e la definizione di nuovi algoritmi crittografici rappresenta solo un tassello all’interno del problema della transizione dell’industria a soluzioni quantum-resistant. Per via dell’uso massiccio della crittografia, in particolare per le comunicazioni internet, un qualsiasi progetto di migrazione coinvolge necessariamente una grossa parte dei sistemi che adoperiamo quotidianamente.
A questo proposito in passato abbiamo già visto come processi analoghi, anche se tipicamente meno strutturali (es. passaggio da 3DES a AES, deprecare MD5), abbiano richiesto almeno un decennio prima di concludersi. In conclusione, è fondamentale che molti dei processi di transizione partano già oggi, in modo da anticiparne le sfide e permettere una rapida adozione dei nuovi standard da parte dell’industria.
Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.
Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.
Gli autori
Edoardo Signorini, laureato in Matematica con curriculum in crittografia presso l’Università di Trento, ha svolto nel 2020 la Tesi Magistrale nell’ambito della Post-Quantum Cryptography (PQC) presso Telsy. Attualmente ricopre il ruolo di crittografo all’interno del gruppo di ricerca di Telsy e svolge un Dottorato di ricerca industriale in Matematica Pura e Applicata presso il Politecnico di Torino. La sua attività si concentra sulla ricerca in ambito PQC e sull’analisi e lo sviluppo di protocolli crittografici.
Giuseppe D’Alconzo, laureato in Matematica con specializzazione in Crittografia presso l’Università di Trento, ha svolto nel 2019 uno stage presso Telsy, occupandosi di Multi-party Computation e Attribute Based Encryption. Attualmente è studente di dottorato in Matematica Pura e Applicata presso il Politecnico di Torino, con una borsa a tema “Crittografia Post-Quantum” nell’ambito del programma UniversiTIM e in collaborazione con il Gruppo di Ricerca di Telsy.
