L’algoritmo quantistico di Shor
Introduzione
Fra le numerose applicazioni del modello di calcolo quantistico, la più rilevante in ambito crittografico è rappresentata dal lavoro dell’informatico americano Peter W. Shor.
Assumendo l’esistenza di un opportuno computer quantistico, con l’articolo pubblicato nel 1995 “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer” Shor ha esposto alla comunità scientifica un algoritmo quantistico in grado di rompere lo schema RSA ed il protocollo Diffie-Hellman, fondamenta della crittografia a chiave pubblica oggi in uso e della maggior parte dei sistemi di comunicazione sicura.
Si pensi, infatti, che tutti gli standard di crittografia a chiave pubblica odierni (es. NIST SP 800-56 A/B, FIPS 186) risulterebbero vulnerabili all’impiego di questo algoritmo. Nel seguito specializzeremo la nostra trattazione sullo schema RSA, il quale basa la propria sicurezza sull’assunzione che il problema matematico della fattorizzazione di numeri interi opportunamente scelti sia computazionalmente intrattabile dagli odierni computer.
Infatti, si stima che, anche sfruttando le più avanzate tecnologie di calcolo classico, per portare a termine la fattorizzazione che romperebbe lo schema RSA a 2048 bit, siano necessari trilioni di anni. D’altra parte, qualora un computer quantistico con determinate caratteristiche in termini di memoria e potenza di calcolo venisse realizzato, l’implementazione dell’algoritmo teorizzato da Shor permetterebbe di completare la stessa fattorizzazione in qualche ora.
Il risultato di Shor è un esempio di speed up esponenziale del modello di calcolo quantistico rispetto al caso classico. L’analisi teorica del miglior algoritmo classico allo stato dell’arte[1] per fattorizzare un numero di n bit stima un costo computazionale di O\Big(e^{c\sqrt[3]{n\log^2{n}}}\Big) operazioni[2] in termini asintotici, mentre l’algoritmo quantistico di Shor ha complessità O(n^2\log{n}\log{\log{n}}). Nello specifico, l’algoritmo classico si dice avere una complessità subesponenziale nel parametro n mentre quello quantistico complessità polinomiale in n.
Simili considerazioni valgono anche per il protocollo Diffie-Hellman in relazione al problema matematico del logaritmo discreto. Di seguito si riporteranno i dettagli tecnici dell’algoritmo quantistico per la fattorizzazione inserendolo in una classe più ampia di problemi.
Per comprendere a pieno la trattazione, si consiglia di riprendere i concetti presentati nell’articolo di introduzione al qubit, mentre per approfondire il tema si segnala un seminario tenuto presso l’associazione De Cifris in collaborazione con Telsy ed il Politecnico di Torino.
Quantum Fourier Transform
Ingrediente fondamentale per la costruzione dell’algortimo di Shor è la Quantum Fourier Transform, analogo quantistico della trasformazione discreta di Fourier. Dato x\in\{0,\dots,2^n-1\}, si definisce la Quantum Fourier Transform dell’n-qubit |x\rangle come QFT(|x\rangle)=\frac{1}{\sqrt{2^n}}\sum_{y=0}^{2^n-1}e^{\frac{2\pi xy}{2^n}}|y\rangle. La definizione è estesa poi per linearità a tutti gli n-qubit. Si può vedere la trasformazione quantistica di Fourier come una distribuzione dell’informazione codificata x in una superposizione di tutti gli n-qubit di base. In seguito sarà utile la seguente osservazione. Dati x, y\in\{0,\dots,2^{n-1}\}, con \sum_{j=0}^{n-1} 2^{j}y_{j} espansione binaria di y, e w_{l}:=e^{\frac{2\pi i}{2^l}}, allora e^{\frac{2\pi i xy}{2^n}}=w_{n}^{xy}=w_{1}^{xy_{n-1}}w_{2}^{xy_{n-2}}\cdots w_{n}^{xy_{0}}. In questi termini, si può riscrivere la Quantum Fourier Transform considerandone esplicitamente l’azione su ciascun qubit. \begin{align*} QFT(|x\rangle) & = \frac{1}{\sqrt{2^{n}}}\sum_{y_{0},\dots y_{n-1}\in\{0,1\}}w_{1}^{xy_{n-1}}\cdots w_{n}^{xy_{0}}|y_{n-1}\dots y_{0}\rangle\\ & = \frac{|0\rangle+w_{1}^{x}|1\rangle}{\sqrt{2}}\frac{|0\rangle+w_{2}^{x}|1\rangle}{\sqrt{2}}\cdots\frac{|0\rangle+w_{n}^{x}|1\rangle}{\sqrt{2}} \end{align*} Il circuito quantistico che calcola la Quantum Fourier Transform è costruito a partire dalla scrittura precedente con l’utilizzo di gate di Hadamard H e Phase Shift R_j controllati, ove per semplicità rispetto al precedente articolo R_j indica R_{2^j}.
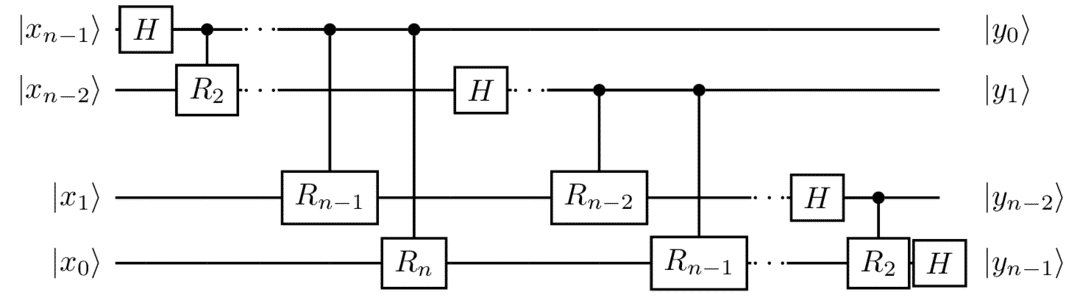
Si noti che al termine del circuito, l’ordine dei qubit risulta invertito e per ristabilirlo andranno applicati dei gate di SWAP.
Quantum Phase Estimation
I problemi che l’algoritmo quantistico di Shor risolve appartengono ad un’ampia classe, detta Quantum Phase Estimation (QPE). La formulazione generale di QPE è la seguente. Data U una trasformazione unitaria e un autostato |\psi\rangle di U determinare la fase \theta\in[0,1) che descrive l’autovalore corrispondente. U|\psi\rangle=e^{2\pi i \theta}|\psi\rangle (Si noti che l’autovalore deve avere questa forma in quanto U è unitaria.) Prima di procedere all’analisi del circuito che risolve la Quantum Phase Estimation, presentiamo due ingredienti chiave per comprendere la successiva discussione.
1. Si consideri il gate cU che agisce come U nel caso in cui il qubit su cui sta controllando sia 1 altrimenti come l’identità. \begin{align*} cU \frac{|0\rangle+|1\rangle}{\sqrt{2}}|\psi\rangle & = \frac{1}{\sqrt{2}}\Big(|0\rangle|\psi\rangle + |1\rangle U|\psi\rangle \Big)\\ & = \frac{1}{\sqrt{2}}\Big(|0\rangle|\psi\rangle+ w_{n}^{2^{n}\theta}|1\rangle|\psi\rangle\Big) \\ & = \frac{|0\rangle + w_{n}^{2^{n}\theta}|1\rangle}{\sqrt{2}} |\psi\rangle \end{align*} In questo modo, il gate cU può essere interpretato come un gate che agisce solo nel primo qubit visto che la seconda parte \ket{\psi} è fissata.
2. Si osservi anche U^{2^{j}}|\psi\rangle = e^{2\pi i 2^j \theta}|\psi\rangle = w_{l-j}^{2^l \theta}|\psi\rangle, \qquad 0\leq j \leq l-1. Il circuito che descrive la soluzione di Quantum Phase Estimation di U è il seguente.
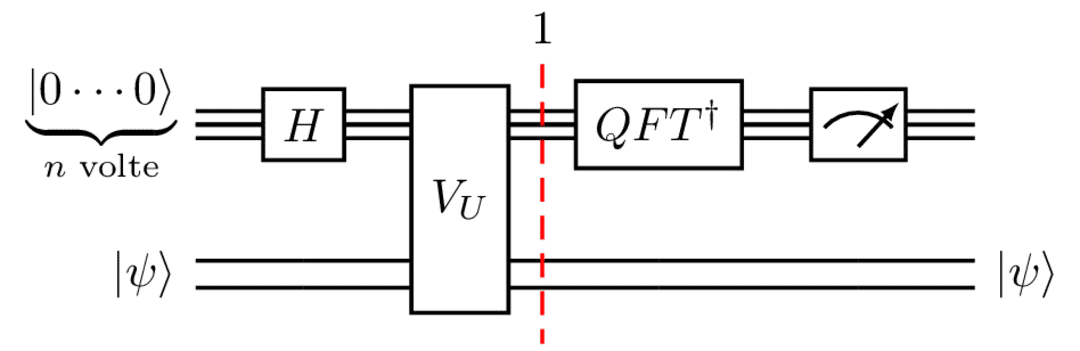
Il gate centrale V_U manda \sum_{x=0}^{2^n-1}|x\rangle|\psi\rangle in \sum_{x=0}^{2^n-1}|x\rangle U^{x}|\psi\rangle. È costruito a partire da 2^{j} gates U agenti sul registro |\psi\rangle controllati dal j-esimo qubit per ogni j. Ad esempio, nel caso n=2 e fissato il registro |10\rangle
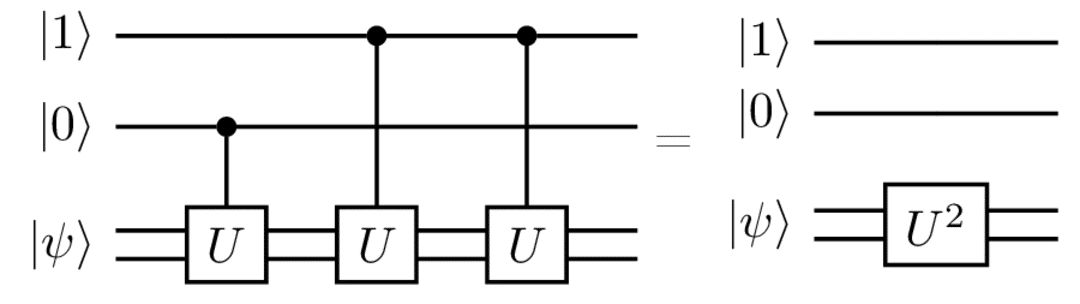
Applicando le n operazioni cU^{2^{j}} con 0\leq j \leq n-1 e sfruttando l’osservazione precedente, l’intero stato ottenuto in 1 è \frac{1}{\sqrt{2^{n}}}\underbrace{(|0\rangle+|1\rangle)}_{n \text{ volte}}|\psi\rangle\longmapsto \frac{|0\rangle+w_{1}^{2^n\theta}|1\rangle}{\sqrt{2}}\frac{|0\rangle+w_{2}^{2^n\theta}|1\rangle}{\sqrt{2}}\cdots\frac{|0\rangle+w_{n}^{2^n\theta}|1\rangle}{\sqrt{2}}|\psi\rangle. Sostituendo 2^n\theta con x nell’espressione sopra riportata si ottiene esattamente la Quantum Fourier Transform di |x\rangle ottenuta nell’osservazione della sezione 2, quindi quanto manca da fare per ritrovare 2^n\theta è applicare l’inversa della Quantum Fourier Transform al primo registro. Il risultato della misura finale è esattamente |2^{n}\theta\rangle. Si noti il ragionamento funziona bene nella situazione in cui 2^{n}\theta sia un intero. Nel caso generale il circuito ritorna solo una stima di \theta da cui si può risalire al valore preciso tramite un procedimento basato sulle frazioni continue.
Algoritmo di Shor
Sia N un intero positivo e sia b un intero coprimo con N, l’obiettivo dell’algoritmo quantistico di Shor è trovare il periodo della funzione f:\,x\mapsto b^{x}\mod N, in un numero di passi polinomiale in \log_{2}{N} passi. Si introducono ora gli ingredienti che permettono di interpretare l’algoritmo di Shor nel contesto della Quantum Phase Estimation. Sia N un intero positivo e a un invertibile modulo N, la trasformazione unitaria considerata è U|y\rangle = |ay \mod N\rangle ove U agisce nello spazio degli m-qubit con m = \lceil \log_{2}{N} \rceil,\qquad n=2m. Un possibile insieme di autostati è dato da |u_{s}\rangle =\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}e^{-\frac{2\pi i sk}{r}}|a^{k} \mod{N}\rangle\qquad s =0,\dots, r-1 ove r è l’ordine moltiplicativo di a, visto che U|u_{s}\rangle=e^{\frac{2\pi is}{r}}|u_{s}\rangle. Chiaramente, se si fosse in grado di ottenere |u_{s}\rangle per qualche s questo vorrebbe dire di essere a conoscenza di r ma questo è l’obiettivo dell’algoritmo. Per ovviare a questo inconveniente, si noti che |1\rangle=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}|u_{s}\rangle.
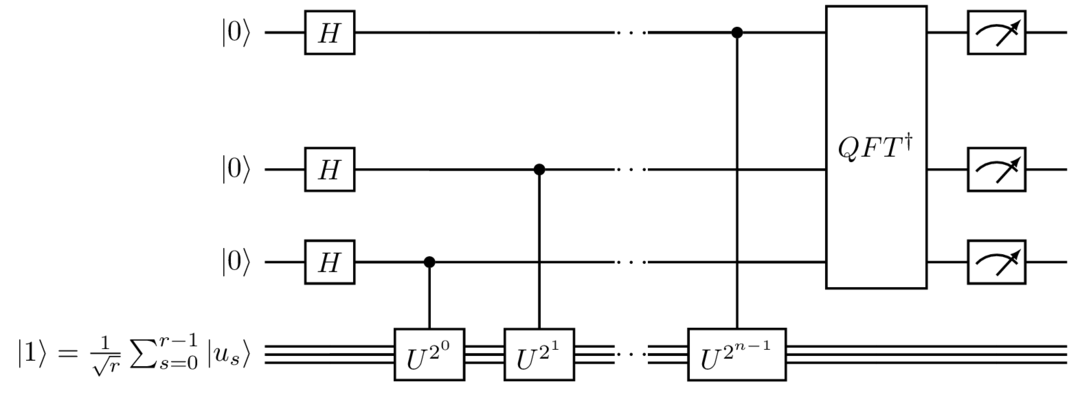
Quindi, se si procede alla QPE di U usando |1\rangle che è una superposizione di r autostati, si misurerà \frac{2^{n}s}{r}, con s un intero casuale fra 0 e r-1. Ragionando per linearità la precedente affermazione è evidente. Di nuovo, nel caso in cui r non sia un divisore di 2^n s si ottiene solo uno stima del valore desiderato e si procederà con le frazioni continue per ritrovarlo.
Soluzione al problema della fattorizzazione
Nello schema crittografico RSA sono considerati prodotti di coppie di primi, quindi N=pq. Si può dimostrare come ci sia un buona probabilità che il periodo ottenuto r sia pari. In questo caso, si ha a^{r}\equiv 1\mod pq,\qquad a^{\frac{r}{2}}\not\equiv 1\mod pq. Con buona probabilità si ha anche a^{\frac{r}{2}}\not\equiv -1\mod pq. A questo punto, siccome (a^{\frac{r}{2}}-1)(a^{\frac{r}{2}}+1)\equiv 0\mod{pq} concludiamo che \{p,q\} = \{\gcd(a^{\frac{r}{2}}-1,N), \gcd(a^{\frac{r}{2}}+1,N)\}.
[1] General Number Field Sieve (GNFS)
Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.
Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.
Gli autori
Edoardo Signorini, laureato in Matematica con curriculum in crittografia presso l’Università di Trento, ha svolto nel 2020 la Tesi Magistrale nell’ambito della Post-Quantum Cryptography (PQC) presso Telsy. Attualmente ricopre il ruolo di crittografo all’interno del gruppo di ricerca di Telsy e svolge un Dottorato di ricerca industriale in Matematica Pura e Applicata presso il Politecnico di Torino. La sua attività si concentra sulla ricerca in ambito PQC e sull’analisi e lo sviluppo di protocolli crittografici.
Francesco Stocco, laureato magistrale in Matematica presso l’Università degli Studi di Padova e l’Université de Bordeaux frequentando il percorso di studi “Algebra Geometry And Number Theory” (ALGANT), entrato a far parte del gruppo di ricerca in Crittografia di Telsy alla fine del 2020 occupandosi in particolare di temi inerenti alle tecnologie quantistiche.
