La negoziazione della chiave nell’era Post-Quantum
Introduzione
La crittografia, intesa come l’insieme di schemi per la protezione dell’informazione, è tipicamente suddivisa in crittografia simmetrica o a chiave privata e in crittografia asimmetrica o a chiave pubblica. Alla crittografia simmetrica afferiscono schemi o protocolli che sfruttano un segreto k (chiave privata) già condiviso fra le parti, comunemente chiamate Alice e Bob.
Ad esempio, nel caso di una comunicazione confidenziale (vedi fig. 1), Alice cifra il messaggio \texttt{msg} che vuole trasmettere combinandolo con il segreto k. Una volta ricevuto il cifrato \texttt{ct}, Bob è in grado di decifrarlo grazie alla conoscenza dello stesso segreto k.
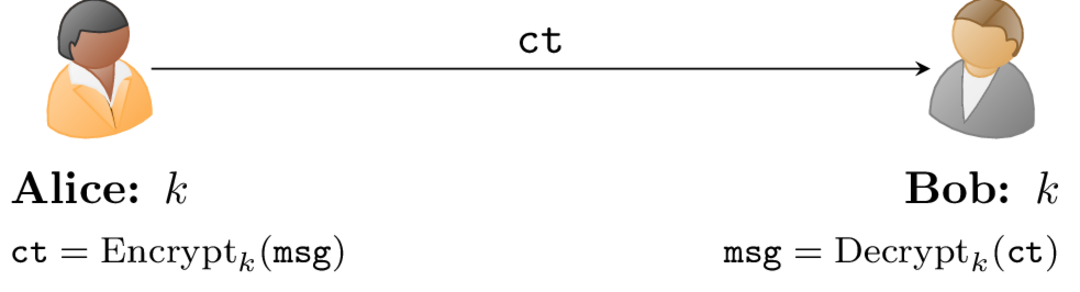
In crittografia asimmetrica, invece, ciascun utente possiede una coppia univoca di chiavi (sk,pk). sk è detta chiave privata e deve essere mantenuta segreta da ogni utente, mentre pk è detta chiave pubblica e può essere condivisa fra le parti.
Nel caso di una comunicazione confidenziale da Alice verso Bob (vedi fig. 2), la coppia di chiavi coinvolte (sk_{\textbf{B}}, pk_{\textbf{B}}) è quella relativa al ricevente. Alice cifra \texttt{msg} con la chiave pubblica di Bob pk_{\textbf{B}} e quest’ultimo è in grado di decifrare \texttt{ct} con la propria chiave privata sk_{\textbf{B}}.
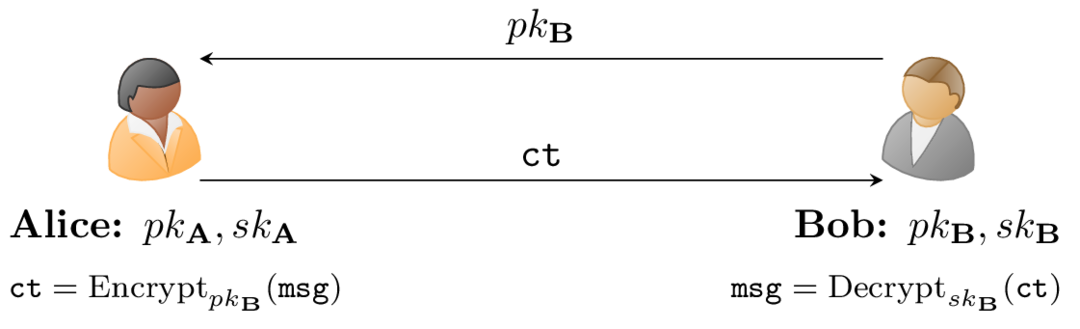
Ad alto livello, quindi, si nota che nel primo caso la stessa chiave è utilizzata sia in fase di cifratura che decifratura, mentre nel secondo due chiavi distinte sono coinvolte.
Le primitive crittografiche simmetriche hanno il vantaggio di essere più efficienti dal punto di vista computazionale. D’altra parte, in crittografia asimmetrica non si assume la disponibilità di un segreto precondiviso da impiegare come chiave crittografica.
Per integrare questi vantaggi, nella pratica le due tecniche sono combinate in schemi crittografici ibridi (vedi fig. 3). La crittografia asimmetrica è utilizzata per la negoziazione di un segreto condiviso e, a partire da questo, la cifratura avviene tramite tecniche di crittografia simmetrica.

Pertanto, la negoziazione di chiavi crittografiche risulta una primitiva fondamentale all’interno dei protocolli di comunicazione sicura. Ad oggi, la tecnica maggiormente diffusa per la sua realizzazione è data dal protocollo crittografico asimmetrico Diffie-Hellman (DH). Oltre a semplicità implementativa ed efficienza, una delle peculiarità che contribuisce alla popolarità del Diffie-Hellman è la sua non-interattività. Infatti, date due parti in comunicazione, queste riescono a stabilire un segreto condiviso da utilizzare come chiave crittografica senza necessità di alcuna interazione, a patto che ciascuna parte conosca la chiave pubblica dell’altra.
Sfortunatamente, assumendo l’esistenza di un opportuno computer quantistico, l’algoritmo di Shor è in grado di rompere completamente i fondamenti matematici alla base di DH impattando largamente la sicurezza della crittografia asimmetrica oggi in uso[1].
In seguito ai primi sviluppi rilevanti delle tecnologie di calcolo quantistico e visto il potenziale impatto catastrofico sulla sicurezza dell’informazione, il NIST ha avviato nel 2017 un processo di standardizzazione per individuare soluzioni di Post-Quantum Cryptography (PQC) ovvero alternative al Diffie-Hellman che siano ritenute resistenti anche al computer quantistico (quantum-resistant). Tuttavia, soluzioni di negoziazione chiave crittografica di tipo non-interattivo basate su fondamenti matematici differenti da quelli del DH si sono dimostrate insicure o generalmente poco mature. Di conseguenza, la valutazione del NIST si è concentrata su meccanismi di scambio chiave con proprietà differenti da quelle garantite da DH, detti Key Encapsulation Mechanisms (KEM).
Un KEM è un protocollo crittografico asimmetrico di scambio chiave di tipo interattivo, infatti anche nel caso in cui le parti conoscano le reciproche chiavi pubbliche, a differenza del DH, almeno una fase di comunicazione è necessaria. In alcuni casi, questa distinzione strutturale fra DH e alternative quantum-resistant costituisce una variazione non banale nel design dei protocolli crittografici, rappresentando una delle sfide della transizione all’era post-quantum.
Le sezioni successive sono dedicate ad una visione ad alto livello del DH e dei KEMs in modo da evidenziare questa differenza.
Diffie-Hellman
Il protocollo Diffie-Hellman vede due parti ottenere lo stesso segreto k, combinando la propria chiave privata con la chiave pubblica dell’interlocutore.
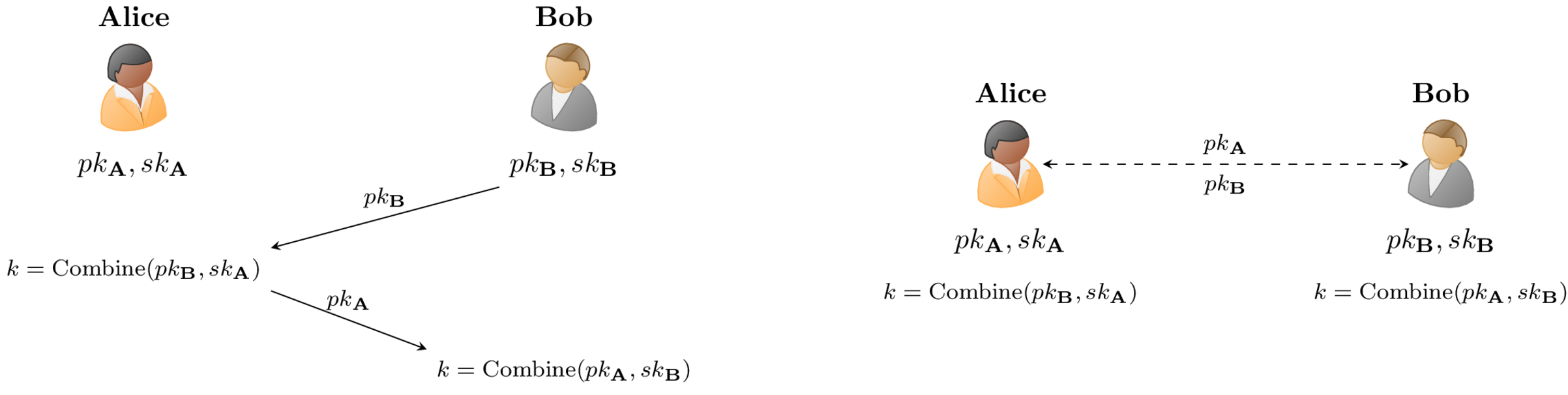
In fig. 4.1, Alice e Bob non conoscono le reciproche chiavi pubbliche pertanto sono necessari due round di comunicazione per portare a termine la negoziazione. Ad esempio, questo utilizzo è comune nel protocollo Transfer Layer Security (TLS) dove ad ogni sessione di comunicazione è necessario che ciascun utente inizializzi una nuova coppia di chiavi dette effimere, in quanto utilizzabili solo durante la relativa sessione.
In fig. 4.2, invece, le reciproche chiavi pubbliche sono note in partenza e non è coinvolta alcuna interazione ulteriore fra le parti per ottenere k. Questo scenario è tipico nel caso in cui le coppie di chiavi coinvolte siano di natura statica o a lungo termine, quindi parte di una Public Key Infrastructure (PKI) oppure salvate in cache in quanto riutilizzabili. L’impiego di sole chiavi statiche è frequente in dispositivi con risorse limitate, ad esempio smartcard, in cui è particolarmente conveniente evitare di generare continuamente nuove coppie di chiavi mantenendone una fissata. L’utilizzo di chiavi effimere offre a priori proprietà di sicurezza aggiuntive ma come appena evidenziato non rappresenta sempre una strada percorribile. Inoltre, anche in protocolli come il TLS dove si fa largo uso di chiavi effimere, per motivi di autenticazione delle parti si osserva parallelamente anche la presenza di chiavi statiche.
Key Encapsulation Mechanism
Sebbene l’obiettivo di un KEM sia il medesimo di DH, ovvero la condivisione fra le parti di un segreto da utilizzare come chiave per cifratura simmetrica, la logica alla base della sua realizzazione è differente. In DH, il ruolo delle due parti coinvolte è sostanzialmente intercambiabile, ciò non si può dire nell’incapsulamento. Un KEM è molto più vicino, nello spirito e nel design, ad una cifratura asimmetrica con il seguente coinvolgimento della coppia di chiavi crittografiche di solo una delle due parti.
In effetti, anche la cifratura stessa del segreto tramite uno schema asimmetrico è una strada percorribile. In genere, però, si tendono a preferire meccanismi di incapsulamento in quanto permettono di evitare agevolmente problematiche di sicurezza che possono sorgere nel momento in cui il segreto da utilizzare come chiave simmetrica viene cifrato in modo asimmetrico.

Analogamente a quanto descritto in precedenza per DH, in fig. 5.1, la prima interazione prevede l’invio di Bob della propria chiave pubblica pk_{\textbf{B}}. In seguito al passaggio di incapsulamento, Alice ottiene il segreto condiviso k e invia un incapsulato \texttt{ct} che, unito alla conoscenza della chiave privata sk_{\textbf{B}}, consentirà a Bob di risalire al medesimo tramite un’ulteriore passaggio di decapsulamento.
In fig. 5.2, invece, si nota che anche nel caso in cui Alice conosca la chiave pubblica di Bob a priori, un’interazione per l’invio dell’incapsulato è comunque necessaria.
Confrontando gli schemi presentati per DH e KEM, si realizza che, in caso di chiavi pubbliche non note a priori, le due strategie sono analoghe in termini di interazioni e, pertanto, ci si aspetta di poter sostituire l’una all’altra negli attuali protocolli crittografici in modo quasi trasparente. D’altro canto, analizzando il caso con chiavi pubbliche note in partenza, il DH non prevede alcuna interazione a differenza di un KEM. In linea più generale, quindi, ciò fa sì che il passaggio all’era post-quantum tramite la sostituzione di DH con KEM quantum-resistant non sia immediato. Inoltre, la transizione è ancora più complessa per quei protocolli crittografici che impiegano variazioni o estensioni di DH, sfruttando le proprietà degli oggetti matematici coinvolti. Questo è il caso della negoziazione chiavi crittografiche Extended Triple Diffie-Hellman (X3DH), utilizzato nel protocollo di messaggistica Signal ad esempio, per cui un cambio di paradigma a KEM non è banale.
Infine, è doveroso ricordare che, pur non essendo una caratteristica intrinseca dei KEM, gli schemi di incapsulamento attualmente considerati nel processo di standardizzazione del NIST sono caratterizzati da chiavi pubbliche di dimensioni molto maggiori rispetto a quelle coinvolte in DH. Tale aspetto non rappresenta un problema dal punto di vista strettamente teorico-crittografico ma dovrà essere tenuto in forte considerazione dal punto di vista implementativo durante la transizione a soluzioni quantum-resistant.
[1] Come discusso nel precedente articolo, il protocollo DH e lo schema RSA costituiscono la quasi totalità della crittografia asimmetrica oggi in uso ed entrambi sono suscettibili all’algoritmo di Shor.
Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.
Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.
Gli autori
Francesco Stocco, laureato magistrale in Matematica presso l’Università degli Studi di Padova e l’Université de Bordeaux frequentando il percorso di studi “Algebra Geometry And Number Theory” (ALGANT), entrato a far parte del gruppo di ricerca in Crittografia di Telsy alla fine del 2020 occupandosi in particolare di temi inerenti alle tecnologie quantistiche.
Marco Rinaudo, laureato triennale in Matematica presso l’Università degli Studi di Torino e studente del corso di laurea magistrale in Matematica con specializzazione in Crittografia presso l’Università di Trento, attualmente stagista nel gruppo di ricerca di Telsy.
