La matematica dietro la PQC: Learning With Errors
Introduzione
Alcuni degli schemi crittografici vincitori del processo di standardizzazione del NIST appartenenti alla famiglia della lattice-based cryptography sono costruiti a partire da un problema detto Learning With Errors (LWE).
Dato un sistema di equazioni lineari random che descrivono un segreto, il problema del Learning With Errors si basa sull’idea di nascondere il valore del segreto aggiungendo del rumore (o errore) al sistema.
Introdotto nel 2005 dall’informatico e matematico teorico israeliano-americano Oded Regev, il LWE ha avuto fin da subito un impatto significativo sulla crittografia post-quantum che ha valso a Regev nel 2018 il Premio Gödel, prestigioso riconoscimento nell’ambito dell’informatica teorica.
Learning With Errors
Nonostante la forte connessione con i problemi sui reticoli, al contrario di ciò che potremmo aspettarci, il LWE non è un problema definito sui reticoli, bensì un problema algebrico.
L’idea del Learning With Errors è quella di rendere difficile un sistema di equazioni random aggiungendo ad esso degli errori.
Per una migliore comprensione del problema, procediamo per gradi considerando il seguente sistema lineare
\begin{cases}
3s_1+3s_2=6 \\
2s_1+5s_2=7 \\
4s_1+s_2=5 \\
\end{cases}
che in forma matriciale può essere riscritto nel seguente modo
\begin{pmatrix}
3 & 3 \\
2 & 5 \\
4 & 1
\end{pmatrix}
\mathbf{s} =
\begin{pmatrix}
6 \\
7 \\
5
\end{pmatrix}
dove \mathbf{s} =
\begin{pmatrix}
s_1 \\
s_2
\end{pmatrix}, costituisce il segreto.
In questo sistema, trovare s risulta computazionalmente facile, in quanto possiamo applicare l’algoritmo di eliminazione di Gauss. Se, invece, al sistema viene aggiunto un errore e= \begin{pmatrix}
e_1 \\
e_2 \\
e_3
\end{pmatrix} con e_i “piccoli”, risolvere
\begin{pmatrix}
3 & 3 \\
2 & 5 \\
4 & 1
\end{pmatrix}
\mathbf{s} +
\begin{pmatrix}
e_1 \\
e_2 \\
e_3
\end{pmatrix}
=
\begin{pmatrix}
4 \\
6 \\
6
\end{pmatrix}
diventa molto difficile.
Nei contesti crittografici, tipicamente ci si restringe agli interi modulo q, dove le operazioni sono implementabili in maniera molto efficiente.
Formalmente, sia q un intero positivo e \mathbb{Z}_q=\{0,\dots,q-1\}, consideriamo m vettori pubblicia_1,\dots,a_m\in \mathbb{Z}_q^k con \mathbf{a}_{i}=(a_{i,1},\dots,a_{i,k}), un segreto \mathbf{s}=(s_1,\dots,s_k)\in \mathbb{Z}_q^k e m valori piccoli e_1,\dots,e_m\in \mathbb{Z}_q e consideriamo il seguente sistema di equazioni:
\begin{cases}
\langle \mathbf{a}_1,\mathbf{s}\rangle+e_1=b_1 \pmod{q} \\
\langle \mathbf{a}_2,\mathbf{s}\rangle+e_2=b_2 \pmod{q} \\
\vdots \\
\langle \mathbf{a}_m,\mathbf{s}\rangle+e_m=b_m \pmod{q}.
\end{cases}
Questo può essere riscritto in forma matriciale nel seguente modo
\begin{pmatrix}
a_{1,1} & \cdots & a_{1,k} \\
a_{2,1} & \cdots & a_{2,k} \\
\vdots & \ddots & \vdots \\
a_{m,1} & \cdots & a_{m,k}
\end{pmatrix}
\cdot
\begin{pmatrix}
s_1 \\
\vdots \\
s_k
\end{pmatrix}
+
\begin{pmatrix}
e_1 \\
e_2 \\
\vdots \\
e_m
\end{pmatrix}
=
\begin{pmatrix}
b_1 \\
b_2 \\
\vdots \\
b_m
\end{pmatrix}
\pmod{q}
che in forma più compatta diventa \mathbf{A}\mathbf{s} + \mathbf{e} = \mathbf{b} \pmod{q}.
Il problema del LWE consiste in, data la coppia (\mathbf{A},\mathbf{b}) dove \mathbf{A} è campionata secondo la distribuzione uniforme ed \mathbf{e} secondo una certa distribuzione di probabilità (che tipicamente è la distribuzione Gaussiana), su \mathbb{Z}_q, trovare \mathbf{s}.
Più nel dettaglio, quella appena enunciata è la versione di ricerca del LWE (Search-LWE) dimostrata essere equivalente dalla versione decisionale (Decision-LWE), in cui l’obiettivo è, data una coppia (\mathbf{A},\mathbf{b}), determinare se questa è della forma appena descritta oppure random.
Osserviamo che, come per l’esempio precedente, la presenza dell’errore \mathbf{e} rende il sistema difficile da risolvere (non è più possibile, ad esempio, calcolare \mathbf{s} mediante l’algoritmo di Gauss). Tale complessità è anche alla base dei sistemi di crittografia a chiave pubblica costruiti a partire dal LWE, con chiave pubblica (\mathbf{A},\mathbf{b}) e chiave privata \mathbf{s}.
Difficoltà del LWE
Il problema LWE gode di una riduzione di complessità al caso medio dal caso peggiore di alcuni problemi sui reticoli, ritenuti difficili sia per i computer classici che quantistici.
In altre parole, la sicurezza del LWE, per opportuni parametri, è garantita a meno che non si possa dimostrare che è sempre possibile risolvere facilmente un’istanza di un problema sui reticoli, cosa che non pare realistica considerati i costi computazionali degli algoritmi attualmente utilizzati per trovare soluzioni.
La difficoltà del problema può essere dimostrata e facilmente intuita a partire da un problema definito sui reticoli detto Bounded Distance Decoding (BDD).
Il BDD è una variante del Closest Vector Problem (CVP) che, dato un reticolo e un vettore (detto target) sufficientemente vicino ad esso nello spazio in cui il reticolo è definito, consiste nel trovare l’unico elemento del reticolo più vicino al target.
Formalmente, dati un reticolo \mathcal{L} e il target \mathbf{t}\in\mathbb{R}^k a distanza piccola d da \mathcal{L}, cioè \min_{x\in\mathcal{L}} \lVert t-x\rVert <d , viene chiesto di trovare \mathbf{x}\in\mathcal{L} tale che \|t-x\|<d.
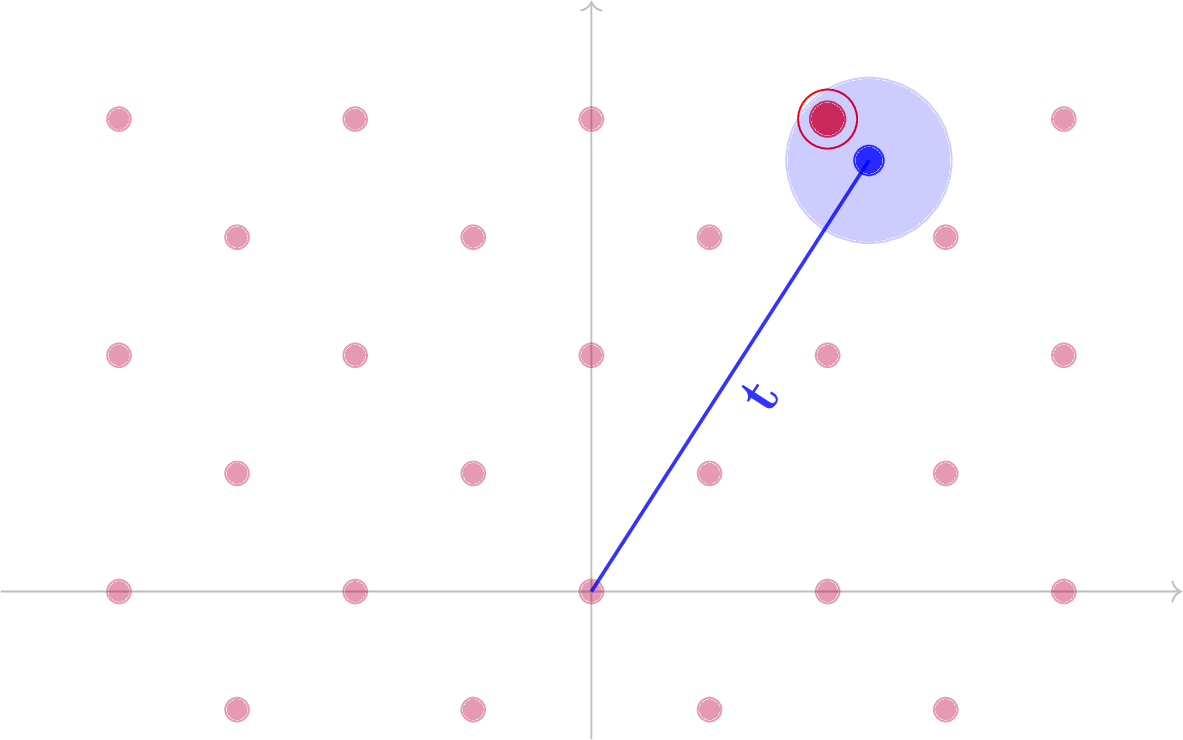
Il BDD, così come gli altri problemi sui reticoli (SVP e CVP) descritti nel precedente articolo di questa rubrica, diventa computazionalmente difficile da risolvere in reticoli di grandi dimensioni, e ad oggi non esiste nessun algoritmo né classico né quantistico in grado di risolvere questi problemi in tempo polinomiale.
Esistono vari risultati teorici che dimostrano che risolvere l’istanza (\mathbf{A},\mathbf{b}) del LWE sia equivalente a risolvere BDD per il reticolo costruito sulla base \mathbf{A} e target \mathbf{b}.
Una semplice intuizione può essere data dal seguente grafico.
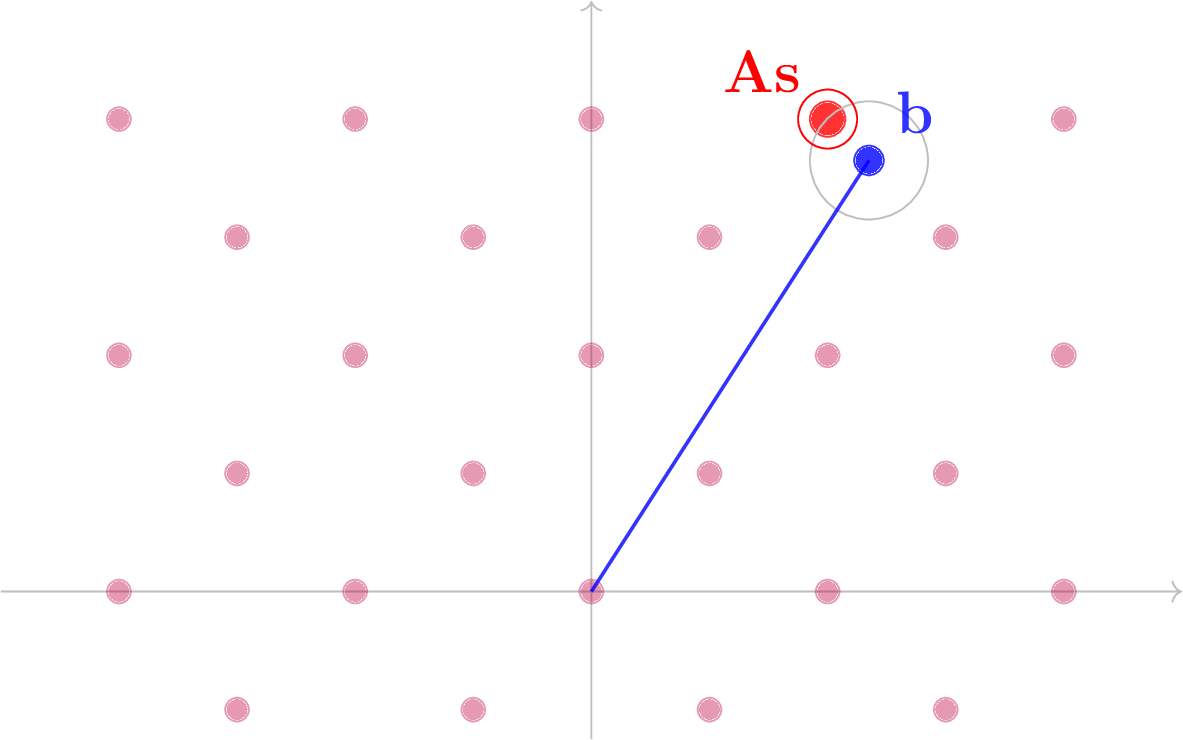
Infatti, sia (\mathbf{A},\mathbf{b}=\mathbf{As}+\mathbf{e}) un’istanza del LWE, definendo il reticolo
\mathcal{L}(\mathbf{A}):=\{\mathbf{Av}:\mathbf{v}\in\mathbb{Z}_q^{k}\},
si nota che, visto che \mathbf{e} è piccolo, \mathbf{As} (da cui è facile ricavare \mathbf{s}) è l’elemento del reticolo \mathcal{L}(\mathbf{A}) più vicino a \mathbf{b}, e si ottiene così un’istanza del BDD.
LWE negli schemi post-quantum
Nel corso degli anni sono state proposte diverse varianti del LWE che sono utilizzate in diverse applicazioni crittografiche.
Gli schemi crittografici basati sul LWE per essere sicuri richiedono chiavi pubbliche di grandi dimensioni, che tipicamente sono dell’ordine di (k\times m) \sim m^2, pari alla dimensione della matrice \mathbf{A}. Ciò significa che al crescere dei parametri di sicurezza cresce quadraticamente la dimensione della matrice \mathbf{A} che compone la chiave pubblica.
Da un punto di vista dell’efficienza, però, è ampiamente desiderabile ridurre la dimensione della chiave pubblica ad un valore che sia al più lineare nei parametri di sicurezza.
Un approccio naturale per raggiungere questo obiettivo è aggiungere una struttura alla matrice pubblica \mathbf{A}, tale che possa essere rappresentata a partire da un’informazione limitata, riducendo quindi lo spazio richiesto per la sua memorizzazione.
A tale proposito, sono state proposte le varianti Ring-LWE e Module-LWE, in cui gli elementi campionati non sono più elementi di \mathbb{Z}_q, come nella versione base LWE, ma di R_q=\mathbb{Z}_q[X]/(X^n+1), lo spazio dei polinomi in X a coefficienti in \mathbb{Z}_q con la relazione X^n=-1.
Su questa seconda, si basa la sicurezza dello schema Kyber, KEM (Key Encapsulation Mechanism) vincitore della competizione del NIST.
Un’istanza del Module-LWE è data da (\mathbf{A},\mathbf{b})\in R_{q}^{m\times k}\times R_{q}^{m} con a_{i,j}(X)\in R_q, s_j(X)\in R_q, e_i\in R_q per ogni i\in\{0,\dots,m\} e per ogni j\in \{0,\dots,k\}.
Per una migliore comprensione, consideriamo come esempio il caso in cui n=2, m=2, k=3. Il generico sistema è definito nel seguente modo:
\begin{pmatrix}
a(X) & c(X) & d(X) \\
f(X) & g(X) & h(X) \\
\end{pmatrix}
\begin{pmatrix}
s_1(X) \\
s_2(X) \\
s_3(X)
\end{pmatrix}
+
\begin{pmatrix}
e_1(X) \\
e_2(X)
\end{pmatrix}
=
\begin{pmatrix}
b_1(X) \\
b_2(X) \\
\end{pmatrix}\in R_{q}^{2}\\
e, più nel dettaglio,
\left(
\begin{array}{c c | c c | c c}
a_0 & -a_1 & c_0 & -c_1 & d_0 & -d_1 \\
a_1 & a_0 & c_1 & c_0 & d_1 & d_0 \\
\hline
f_0 & -f_1 & g_0 & -g_1 & h_0 & -h_1 \\
f_1 & f_0 & g_1 & g_0 & h_1 & h_0
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
s_{1,0} \\
s_{1,1} \\
\hline
s_{2,0} \\
s_{2,1} \\
\hline
s_{3,0} \\
s_{3,1}
\end{array}
\right)
+
\left(
\begin{array} {c }
e_{1,0} \\
e_{1,1} \\
\hline
e_{2,0} \\
e_{2,1}
\end{array}
\right)
=
\left(
\begin{array}{c}
b_{1,0} \\
b_{1,1} \\
\hline
b_{2,0} \\
b_{2,1}
\end{array}
\right) \in \mathbb{Z}_{q}^{2\cdot 2}
Di ognuno di questi problemi, esiste anche la versione derandomizzata, dove gli errori sono introdotti da un’operazione di rescaling e arrotondamento, dando luogo al problema del Learning With Rounding (LWR) e alle varianti Ring-LWR e Module-LWR. Su quest’ultima si basa la sicurezza di Saber, KEM che è stato escluso dalla competizione del NIST al termine del terzo round, a favore di Kyber.
Oltre al largo utilizzo nella lattice-based cryptography, il LWE permette di costruire una grande varietà di primitive crittografiche, tra cui schemi di Fully Homomorphic Encryption (FHE).
Nel corso dei prossimi articoli di questa rubrica si approfondiranno il KEM Kyber e la firma Dilithium, vincitori della prima fase del processo di standardizzazione del NIST che si basano su varianti del LWE.
Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.
Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.
Gli autori
Veronica Cristiano, laureata triennale in Matematica presso l’Università di Pisa e laureata magistrale in Matematica con specializzazione in Crittografia presso l’Università di Trento, entrata a far parte del gruppo di ricerca in Crittografia di Telsy a metà del 2021.
Francesco Stocco, laureato magistrale in Matematica presso l’Università degli Studi di Padova e l’Université de Bordeaux frequentando il percorso di studi “Algebra Geometry And Number Theory” (ALGANT), entrato a far parte del gruppo di ricerca in Crittografia di Telsy alla fine del 2020 occupandosi in particolare di temi inerenti alle tecnologie quantistiche.

