La matematica dietro la PQC: i reticoli

Introduzione

Un grande numero di schemi di crittografia post-quantum è costruito su una struttura matematica detta reticolo, sulla quale possono essere definiti problemi difficili da risolvere anche per un computer quantistico.

I crittosistemi appartenenti a questa classe, la cosiddetta lattice-based cryptography (lattice è il termine inglese che denota un reticolo), basano la propria sicurezza su alcuni noti problemi computazionali studiati da diversi decenni e congetturati intrattabili sia in presenza di computer classici che quantistici.

Durante il processo di standardizzazione del NIST volto ad individuare nuovi schemi nell’ambito della crittografia a chiave pubblica che siano quantum-resistant sono stati proposti numerosi schemi basati sui reticoli.

Vista la loro sicurezza e la loro notevole efficienza, molti di questi hanno prevalso nelle fasi avanzate della selezione: tre dei quattro vincitori, il KEM (Key Encapsulation Mechanism) Kyber e le firme digitali Dilithium e Falcon, sono basati sui reticoli.  

I reticoli

I reticoli sono oggetti geometrici che possono essere intuitivamente descritti come una griglia.

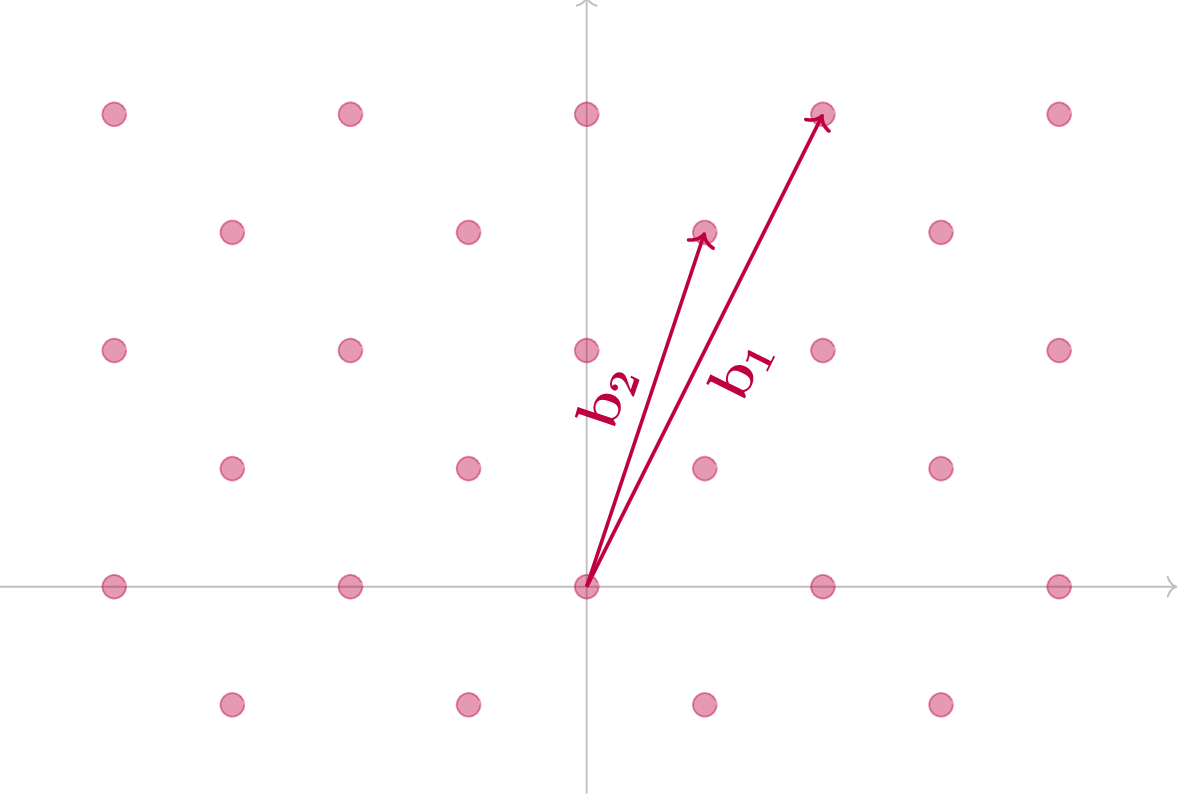
Formalmente, dato un insieme di vettori linearmente indipendenti B = \{b_1,\dots ,b_r\} in \mathbb{R}^n , il reticolo \mathcal{L}(B) è definito come l’insieme delle combinazioni lineari a coefficienti interi dei vettori contenuti in B .

In altre parole, \mathcal{L}=\{x_1 b_1+x_2 b_2+\dots +x_r b_r| x_1,\dots,x_r\in\mathbb{Z}\} . Per semplicità possiamo pensare ad un reticolo come ad un insieme di punti dello spazio n-dimensionale con struttura periodica.

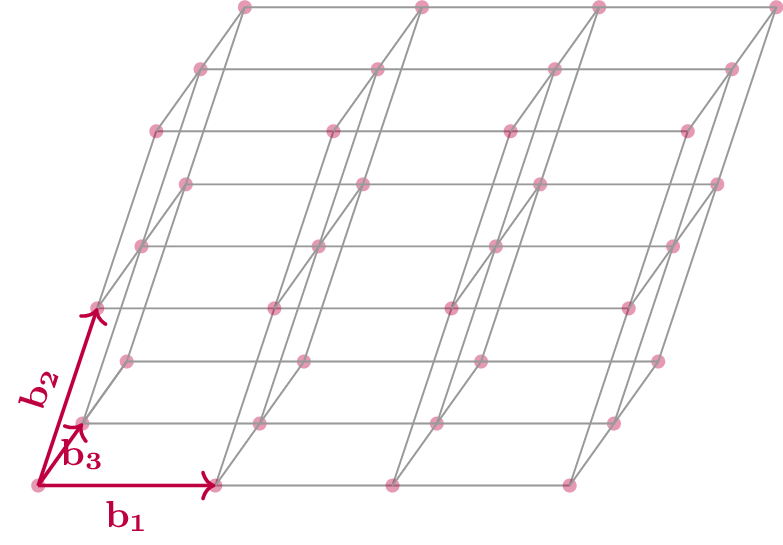
Nella figura sottostante possiamo vedere il caso di un reticolo in uno spazio di dimensione 2 (e con r=2 ) e di uno nello spazio di dimensione 3 (e con r=3 ).  

Problemi computazionali sui reticoli

Come abbiamo detto in precedenza, sui reticoli è possibile definire alcuni problemi computazionali sulla cui difficoltà di risoluzione si basa la sicurezza degli schemi di lattice-based cryptography. Due di questi sono lo Shortest Vector Problem (SVP) e il Closest Vector Problem (CVP).

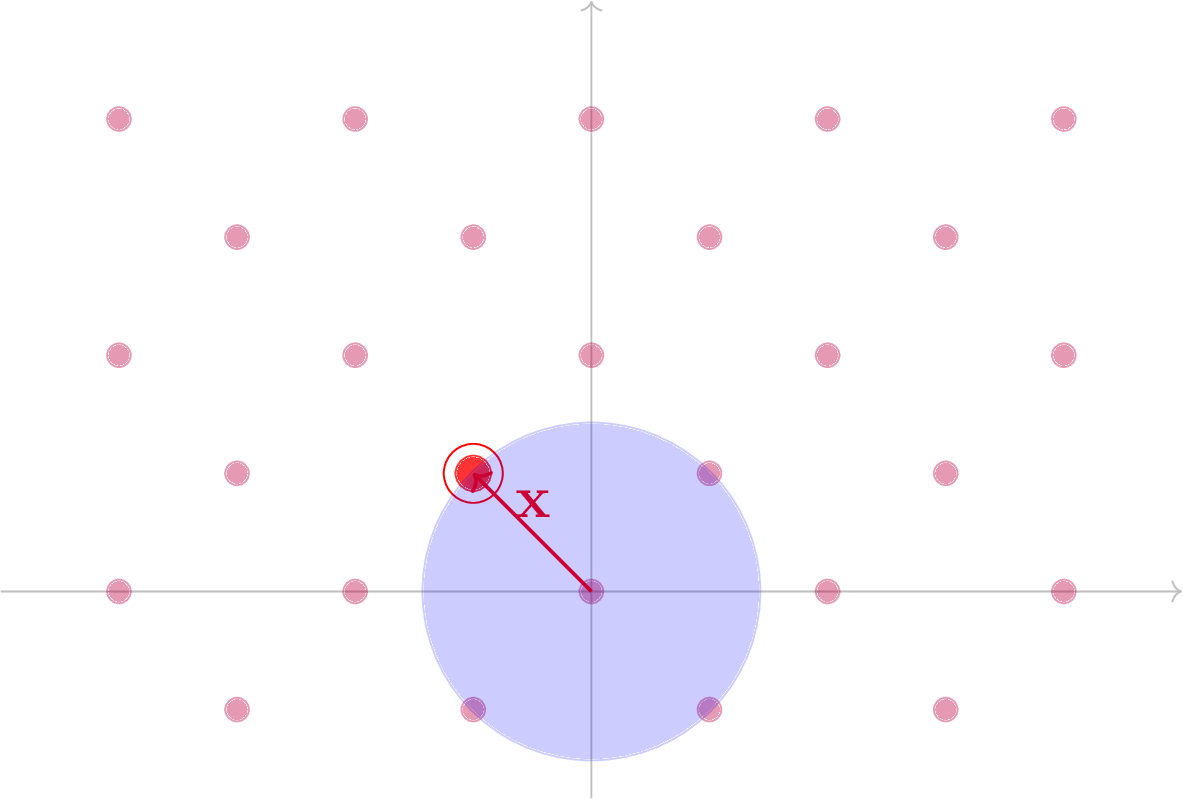
Lo Shortest Vector Problem è il problema di trovare un elemento del reticolo (non nullo) avente distanza minima dall’origine. Formalmente, dato un reticolo \mathcal{L} \subset \mathbb{R}^n , l’obiettivo è trovare x\in \mathcal{L} tale che \| x\| = \min_{t \in \mathcal{L}\setminus \{0\}} \| t\|.

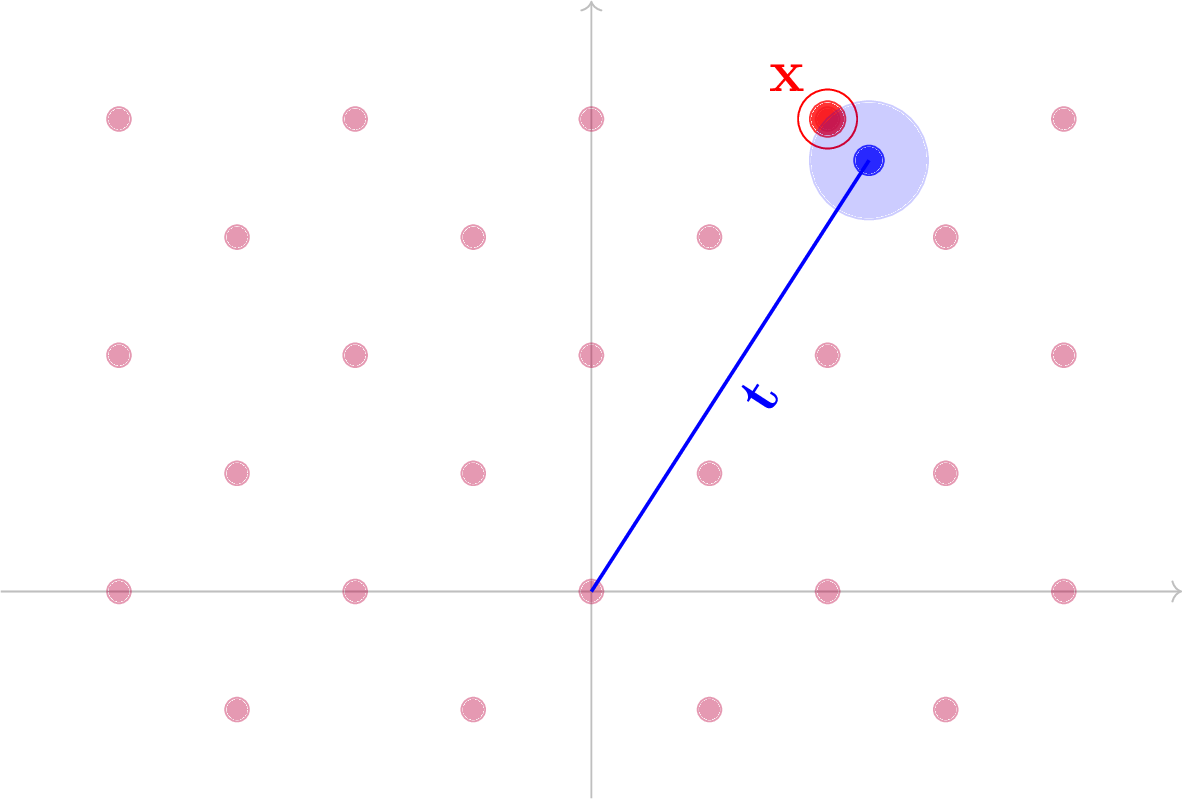
Il secondo problema computazionale su cui si basano molti crittosistemi è il cosidetto Closest Vector Problem il cui obiettivo consiste nel trovare l’elemento nel reticolo più vicino ad un dato vettore nello spazio in cui il reticolo è definito.

Formalmente, dato un reticolo \mathcal{L} \subset \mathbb{R}^n e un vettore t\in \mathbb{R}^n che non appartiene a \mathcal{L} , viene chiesto di trovare l’elemento x \in \mathcal{L} tale che \lVert x-t\rVert = \min_{a\in \mathcal{L}} \lVert a-t \rVert.

Sia per il CVP che per il SVP è possibile anche definire delle versioni approssimate ( \gamma -CVP e \gamma -SVP), in cui viene richiesto di trovare una soluzione a meno di un fattore \gamma , che solitamente dipende dalla dimensione del reticolo stesso.

Le versioni esatte dei problemi appena descritti appartengono ad una classe di problemi estremamente difficili (noti come problemi NP-completi), i quali trovano però difficile applicazione in ambito crittografico.

Per questa ragione la sicurezza degli schemi crittografici basati su reticoli si riduce tipicamente alla complessità delle versioni approssimate di SVP e CVP per opportuni fattori di approssimazione. 

Difficoltà dei problemi

Nonostante esistano diversi algoritmi di risoluzione, SVP e CVP diventano computazionalmente difficili da risolvere in reticoli di grandi dimensioni. Attraverso l’analisi del costo computazionale di tali algoritmi è possibile comprendere la difficoltà della risoluzione di CVP e SVP e quindi stimare la sicurezza dei crittosistemi di lattice-based cryptography basati su essi.

Tra gli algoritmi di risoluzione di CVP e SVP maggiormente diffusi possiamo citare LLL (Lenstra, Lenstra, Lovasz), proposto nel 1982, e la sua generalizzazione BKZ (proposto da Schnorr e Euchner), oggi più utilizzato.

Questi, però, sono in grado di risolvere in tempo polinomiale solamente la versione approssimata di SVP per valori di \gamma troppo elevati per poter essere utilizzati in un attacco reale ai danni degli schemi basati sui reticoli.

Possiamo inoltre ricordare gli algoritmi proposti da Kannan (1983) e Babai (1986), anche questi capaci di risolvere in tempo polinomiale la versione approssimata di CVP per fattori di approssimazione esponenziali nella dimensione del reticolo considerato.

Gli algoritmi in grado di trovare soluzioni per SVP e CVP con fattori di approssimazione polinomiali (il caso di riferimento per la lattice-based cryptography) richiedono un tempo esponenziale nella dimensione del reticolo e perciò non è possibile realizzare attacchi efficaci nei confronti degli attuali schemi basati sui reticoli.

I reticoli alla base della PQC

A sostegno della sicurezza della lattice-based cryptography vi è un peculiare risultato teorico che lega la complessità nel caso medio degli schemi crittografici ai casi “peggiori” di alcuni problemi sui reticoli.

Con complessità nel caso medio si fa riferimento a classi di problemi per i quali la scelta randomica di parametri non ne influenza in media la complessità. Tali problemi sono di interesse nella crittografia a chiave pubblica in quanto ad ogni generazione di chiave è implicitamente associata un’istanza randomica di un problema, la cui sicurezza non deve dipendere dalla scelta di tale istanza.

D’altra parte, la nozione di caso peggiore, per la quale un problema è ritenuto difficile a patto che vi sia almeno un’istanza computazionalmente intrattabile, risulta maggiormente intuitiva e di più semplice analisi ma è irrilevante ai fini crittografici.

Nel 1996 il matematico ungherese Miklos Ajtai ha dimostrato la riduzione da caso peggiore a caso medio, attraverso la quale è possibile definire alcune costruzioni (su cui si basa la sicurezza dei crittosistemi di lattice-based cryptography) che risultano difficili a meno che tutte le istanze di alcuni problemi sui reticoli (ad esempio SVP e CVP) siano facili da risolvere.

Questo risultato, sebbene di carattere teorico e non immediatamente applicabile agli schemi oggi esistenti, rafforza la fiducia nel design di costruzioni crittografiche basate sui reticoli.

Infatti, la sicurezza di queste per opportuni parametri è garantita a meno che non si possa dimostrare che è sempre possibile risolvere facilmente un’istanza di SVP o di CVP, cosa che non pare realistica considerati i costi computazionali degli algoritmi attualmente utilizzati per trovare soluzioni a questi problemi.

Inoltre, nonostante i numerosi tentativi compiuti a partire dagli anni ‘90, non sono stati proposti algoritmi quantistici che risolvono CVP e SVP con prestazioni nettamente migliori degli algoritmi classici sopra citati.

Questo fatto supporta la convinzione diffusa nella comunità matematica che questi problemi computazionali possano costituire la base adatta su cui sviluppare schemi crittografici resistenti ad attacchi di un computer quantistico e a cui affidare il futuro della crittografia a chiave pubblica.

A testimonianza di ciò si può notare la predominanza di schemi basati sui reticoli nel processo di standardizzazione indetto dal NIST: nel primo round della competizione tali schemi erano 26 su un totale di 64, nel secondo round 12 su un totale di 26 e nel terzo round 7 su 15.

Nel corso dei prossimi articoli di questa rubrica si approfondiranno i tre vincitori della prima fase del processo di standardizzazione del NIST basati sui reticoli: Kyber, Dilithium e Falcon.

Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.

Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.

Gli autori

Veronica Cristiano, laureata triennale in Matematica presso l’Università di Pisa e laureata magistrale in Matematica con specializzazione in Crittografia presso l’Università di Trento, entrata a far parte del gruppo di ricerca in Crittografia di Telsy a metà del 2021.

Marco Rinaudo, laureato triennale in Matematica presso l’Università degli Studi di Torino e laureato magistrale con specializzazione in Crittografia presso l’Università di Trento. In seguito ad uno stage curricolare svolto nel 2022 in Telsy, da gennaio 2023 è parte del Gruppo di Ricerca in Crittografia.