Il qubit logico e la correzione degli errori quantistici

18 Mag

Qubit fisico vs qubit logico

Come discusso nel precedente articolo, l’unità di informazione elaborata da un computer quantistico è genericamente detta Qubit o Bit Quantistico.

Tuttavia, per una comprensione più profonda delle problematiche legate alla realizzazione di un computer quantistico, è necessario introdurre e distinguere le nozioni di qubit fisico e qubit logico.

All’interno di un processore quantistico, ciascun qubit fisico è in corrispondenza uno ad uno con lo stato quantistico di una particella o, più in generale, di un fenomeno microscopico che lo codifica. Esistono varie tipologie di qubit fisico a seconda della tecnologia di codifica. A titolo di esempio, fra i più noti, si citano i qubit fisici a superconduttori, a ioni intrappolati e a fotoni.
Il qubit fisico è un’entità instabile. Infatti, ogni tentativo di condurre il qubit fisico alle computazioni desiderate tramite azioni esterne può causare l’alterazione dello stato quantistico vanificando la bontà dell’informazione codificata.

Per mitigare questa problematica, più qubit fisici vengono fatti interagire con l’obbiettivo di mantenere stabile nel tempo un unico stato quantistico su cui sia possibile agire in modo non distruttivo. Un insieme di qubit fisici con questa caratteristica viene definito qubit logico. Il qubit logico è un’entità teorica corrispondente alla reale unità di informazione quantistica che un processore quantistico è in grado di controllare ed il numero di qubit logici ne identifica l’effettiva capacità di calcolo associata. Per realizzare il qubit logico si ricorre all’applicazione di codici di correzione di errori quantistici (Quantum Error Correction), in modo simile a quanto accade per gli errori di trasmissione dei bit classici.

Il dualismo qubit fisico-logico è un tema ancora poco chiaro allo stato dell’arte, la questione fondamentale da affrontare è la stima precisa del numero di qubit fisici necessari a realizzarne uno logico. Tale stima dipende, anzitutto, dalla tecnologia quantistica intesa sia come stato di avanzamento tecnologico sia come tecnologia di codifica dei qubit fisici. Al momento non c’è motivo di pensare che un’eventuale stima possa valere allo stesso tempo per diverse tecnologie, anzi è ragionevole immaginare che sistemi di natura differente presentino comportamenti molto diversi in tal senso. Ad esempio, i qubit fisici a superconduttori sono molto più instabili di quelli a ioni intrappolati, sebbene garantiscano altri vantaggi implementativi. In secondo luogo, anche la complessità del circuito quantistico che si desidera implementare influisce su questa stima. Più il tempo di esecuzione del circuito è lungo, più il tempo in cui qubit logico si mantiene stabile deve essere esteso e di conseguenza più qubit fisici saranno necessari a tal fine.

Di seguito si riporta una considerazione che può essere utile per dare concretezza a quanto appena descritto, la stima fornita non è da intendersi come assoluta viste le precedenti osservazioni ma dà un’idea degli ordini di grandezza sottostanti al problema. Seguendo l’implementazione dell’algoritmo quantistico di Shor proposta in [1], per rompere una chiave RSA a 2048 bit servirebbero 14238 qubit logici^[2]. Si suggerisce che a ciascun qubit logico corrispondano 1583 qubit fisici a superconduttori, il risultato è una rottura di RSA-2048 sfruttando circa 20 milioni di qubit fisici.

Nella sezione successiva è trattato un esempio di Quantum Error Correction in un caso elementare ai fini di fornire un’idea significativa di quanto accade in generale. Per il formalismo matematico relativo ai qubit ed ai circuiti quantistici si fa riferimento al precedente articolo della rubrica.

Quantum Error Correction

La correzione degli errori è una tecnica fondamentale anche in computazione classica. Talvolta, l’informazione codificata in stringhe di variabili binarie (bit) risulta perturbata, generalmente a causa di alterazioni durante la trasmissione. Una possibile strategia basilare di mitigazione è quella di codificare ciascun bit logico in sequenze di tre bit fisici^[4].
$\begin{align*}\bar{0} & \longleftrightarrow 000 \\ \bar{1} & \longleftrightarrow 111\end{align*}$
Con l’assunzione che la simultanea alterazione di più di un bit fisico sia improbabile all’interno di un’unica sequenza di tre bit fisici, la correzione avviene monitorando il loro stato che in principio dovrebbe mantenersi identico. Qualora un’alterazione venisse rilevata, il valore presumibilmente corretto è ristabilito confrontando i tre bit fisici e seguendo un criterio di maggioranza. Ad esempio, nel caso si rilevasse una sequenza di bit fisici $001$ questa verrebbe corretta in $000$ , in quanto l’occorrenza di $0$ in $001$ è prevalente. Tale alterazione, unica possibile nel caso classico, è detta bit flip. Nel caso quantistico, invece, le proprietà del qubit fanno sì che il (qu)bit flip non sia l’unica alterazione da cui difendersi, per citare un esempio si considerino gli errori di fase, e.g., $|\psi\rangle\rightarrow e^{i\theta}|\psi\rangle$ . Tuttavia, in questo articolo si tratterà solo il caso di bit flip in quanto sufficiente a dare un’idea significativa anche del caso generale.

Un’applicazione del tutto analoga alla tecnica di correzione degli errori classica non è percorribile nel caso quantistico. In calcolo quantistico, il monitoraggio classico dei bit fisici si tradurrebbe in una misurazione dei qubit fisici che per sua natura andrebbe a perturbarne lo stato vanificando ogni sforzo di correzione. Una strategia di calcolo quantistico alternativa alla misura per la correzione di bit flip è riportata in dettaglio di seguito.

Dato un qubit logico $|\psi\rangle$ , la prima operazione consiste nella sua codifica in una sequenza di tre qubit fisici, ciascuno rappresentato da una riga del seguente circuito.

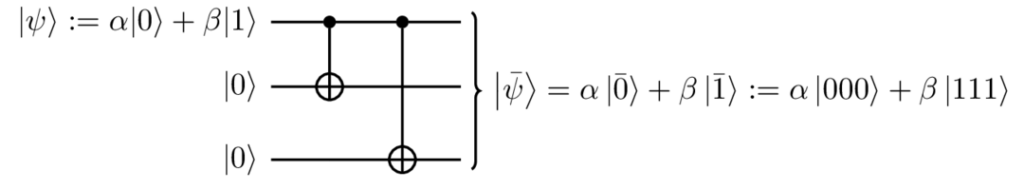
In un circuito quantistico, l’errore di bit flip può essere modellizzato dalla presenza di un NOT gate estraneo, indicato con $X$ .

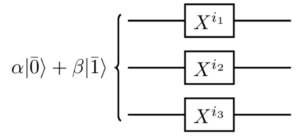
Formalmente, per denotare il fatto che si sta considerando al più un bit flip, si ha
$i_j\in\{0,1\}\,\forall j,\qquad \sum_{j=1}^{3}i_j \leq 1.$
Di conseguenza il qubit $|\bar{\psi}\rangle$ può risultare alterato in uno dei seguenti stati:
$\begin{align*}|\bar{\psi}_1\rangle & :=\alpha|001\rangle+\beta|110\rangle, \\|\bar{\psi}_2\rangle & :=\alpha|010\rangle+\beta|101\rangle, \\|\bar{\psi}_3\rangle & :=\alpha|100\rangle+\beta|011\rangle.\end{align*}$
La correzione di tali istanze è possibile grazie all’introduzione di due qubit fisici ausiliari. L’idea è di “registrare l’errore” su questi due qubit, misurarli e operare di conseguenza. Il circuito risultante è il seguente, in cui le prime due righe corrispondono ai due qubit ausiliari inizializzati a $|0\rangle$ .

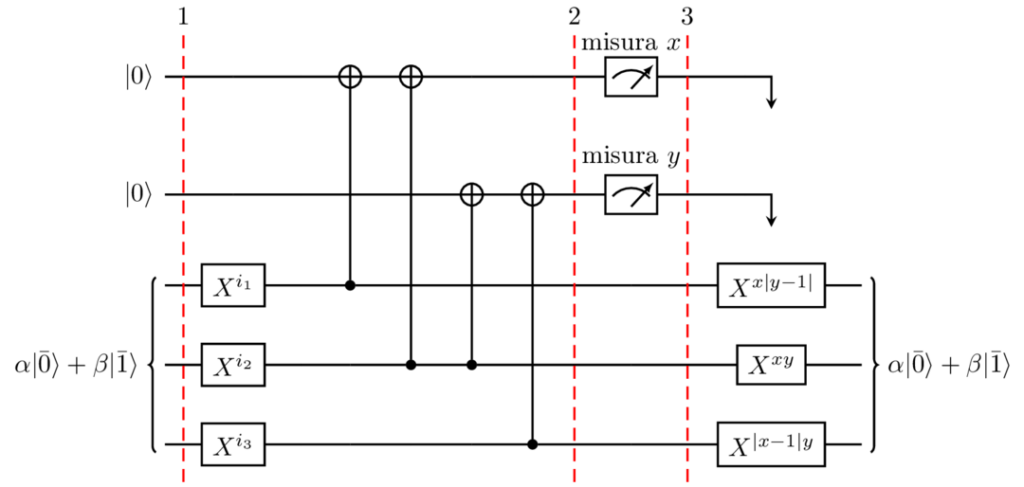
Affinché il circuito risulti corretto l’azione dei NOT gate posti al passaggio $3$ , a seconda del risultato della misura in $2$ , deve annullare l’alterazione modellizzata al passaggio $1$ , quindi si dovrà ottenere
$\begin{align*}i_1 & =x\cdot|y-1|;\\i_2 & =x\cdot y;\\i_3 & =|x-1|\cdot y.\end{align*}$
Si consideri il caso in cui $|\bar{\psi}\rangle$ sia alterato in $|\bar{\psi_1}\rangle$ , i.e., $i_3=1,i_1=i_2=0$ , la trattazione delle altre istanze è del tutto analoga. Verificando che $x=0, y=1$ , seguono tutte le uguaglianze sopra richieste.
Infatti, l’azione dei quattro CNOT sullo stato $|00\rangle|\bar{\psi_1}\rangle$ è la seguente, da cui è immediata la conclusione.
$\begin{align*}\text{I CNOT } && |00\rangle|\bar{\psi_1}\rangle & \longmapsto \alpha|00001\rangle+\beta|10110\rangle\\ \text{II CNOT } && & \longmapsto \alpha|00001\rangle+\beta|00110\rangle\\ \text{III CNOT } && & \longmapsto \alpha|00001\rangle+\beta|01110\rangle\\ \text{IV CNOT } && & \longmapsto \alpha|01001\rangle+\beta|01110\rangle=|01\rangle|\bar{\psi_1}\rangle\implies x=0, y=1\end{align*}$

Una generica alterazione di 1-qubit può essere vista come una combinazione di bit flip ed errore di fase, formalmente
$|\psi\rangle\longmapsto(\alpha \mathbf{1} + \beta X + \gamma Z + \delta ZX)|\psi\rangle$
ove $|\alpha|^2+|\beta|^2+|\gamma|^2+|\delta|^2=1$ e $Z|x\rangle=(-1)^x|x\rangle$ . Una generalizzazione della precedente discussione sul bit flip consente di produrre un circuito quantistico che corregga questo errore generico sfruttando 9 qubit fisici (5 per la codifica di $|\psi\rangle$ e 4 ausiliari).

Tuttavia, per coprire tutti i casi possibili è necessario tenere in considerazione anche errori modellizzati da gate che agiscano correlando fra loro più qubit fisici. Inoltre, l’assunzione per cui la probabilità di avere più di un errore in una sequenza di tre qubit fisici sia trascurabile non è realistica allo stato attuale della tecnologia. Queste ragioni sono alla base della stima numero di qubit fisici per qubit logico riportata nella precedente sezione.

[ 1 ] Gidney, Ekerå, How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits, 2019.
[ 2 ] Non si tratta di una soluzione ottimale da questo punto di vista, ad esempio in [3] l’algoritmo presentato si appoggerebbe a 4099 qubit logici, ma si tratta di un trade off per mitigare anche il costo computazionale complessivo dell’algoritmo in termini di gate quantistici.
[ 3 ] Beauregard S., Circuit for Shor’s algorithm using 2n+3 qubits, Quantum Information and Computation, Vol. 3, No. 2, 175-185, 2003.
[ 4 ] Il dualismo bit fisico – bit logico è analogo a quanto discusso in precedenza per i qubit.

Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.

Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.

Gli autori

Edoardo Signorini, laureato in Matematica con curriculum in crittografia presso l’Università di Trento, ha svolto nel 2020 la Tesi Magistrale nell’ambito della Post-Quantum Cryptography (PQC) presso Telsy. Attualmente ricopre il ruolo di crittografo all’interno del gruppo di ricerca di Telsy e svolge un Dottorato di ricerca industriale in Matematica Pura e Applicata presso il Politecnico di Torino. La sua attività si concentra sulla ricerca in ambito PQC e sull’analisi e lo sviluppo di protocolli crittografici.

Francesco Stocco, laureato magistrale in Matematica presso l’Università degli Studi di Padova e l’Université de Bordeaux frequentando il percorso di studi “Algebra Geometry And Number Theory” (ALGANT), entrato a far parte del gruppo di ricerca in Crittografia di Telsy alla fine del 2020 occupandosi in particolare di temi inerenti alle tecnologie quantistiche.