Falcon: firma digitale basata su NTRU
Introduzione
Il processo di standardizzazione del NIST in ambito Post-Quantum ha identificato due schemi crittografici basati sulla teoria dei reticoli nell’ambito delle firme digitali: CRYSTALS-Dilithium e Falcon.
All’interno dei moderni protocolli crittografici di comunicazione, queste soluzioni sostituiranno gli schemi attualmente utilizzati per la firma digitale, vulnerabili agli attacchi di un computer quantistico.
Se da un lato Dilithium è stato selezionato come soluzione primaria, Falcon può rivelarsi più adeguato in particolari scenari applicativi come evidenziato dal NIST. Ad esempio, elemento più favorevole a Falcon è la possibilità di trasmettere una firma in un singolo pacchetto IP, evitando problematiche legate alla frammentazione.
D’altra parte, il design di Falcon è più complesso da comprendere ed implementare. La costruzione è basata su tre ingredienti principali: il problema matematico NTRU, il framework GPV per firme digitali hash-and-sign basate su reticoli e il metodo di campionamento firma Fast Fourier Sampling.
NTRU Problem
Sia n una potenza di 2 e q un numero primo, un insieme di segreti \text{NTRU} è costituito da quattro polinomi piccoli[1]
f,g,F,G\in\mathbb{Z}[X]/(X^n+1)
tali che
fG-gF=q\mod{X^n+1}
e f è invertibile modulo q.
In questo scenario, la chiave segreta sarà costituita da (f,g,F,G) mentre la chiave pubblica dal polinomio
h = g\cdot f^{-1}\mod q.
Il problema \text{NTRU}, considerato difficile da risolvere anche per un computer quantistico, risiede nell’individuare due polinomi a piccoli coefficienti f', g' tali che h coincida con g'f'^{-1} modulo q.
Tale problema è strettamente collegato alla teoria dei reticoli, in quanto il miglior algoritmo crittoanalitico noto consiste nella risoluzione di un’istanza di Shortest Vector Problem (SVP) nel reticolo generato dalla matrice 2n \times 2n a coefficienti interi
\begin{bmatrix}
1&h\\
0&q\\
\end{bmatrix}
:=
\left(\begin{array}{c c c c | c c c c}
1&0&\cdots&0&h_0&h_1&\cdots&h_{n-1}\\
0&1&\cdots&0&-h_{n-1}&h_0&\cdots&h_{n-2}\\
\vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\ddots&\vdots\\
0&0&\cdots&1&-h_1&-h_2&\cdots&h_0\\
\hline
0 & 0 & \cdots & 0 & q & 0 & \cdots & 0 \\
0 & 0 & \cdots & 0 & 0 & q & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 0 & 0 & 0 & \cdots & q
\end{array}\right),
ove h=h_0+h_1X+\cdots+h_{n-1}X^{n-1}.
Framework GPV
Il framework GPV, proposto da Gentry, Peikert e Vaikuntanathan nel 2008, fornisce una linea guida per la realizzazione di uno schema di firma digitale sicuro basato sui reticoli e sul paradigma hash-and-sign[2].
Ad alto livello, il framework prevede una chiave pubblica costituita da una matrice di rango massimo
\mathbf{A}\in\mathbb{Z}_{q}^{n\times k}, k>n
e una chiave privata costituita da una matrice
\mathbf{B}\in\mathbb{Z}_{q}^{k\times k}\text{ tale che }\mathbf{BA}^{T}=\mathbf{0}.
Data \text{H}:\{0,1\}^{*}\rightarrow\mathbb{Z}_q^n funzione di hash, la firma di un dato messaggio m è data da un piccolo vettore \mathbf{s} in \mathbb{Z}_q^k tale che
\mathbf{sA}^{T}=\text{H}(m).
Se il processo di verifica è agevole, basta controllare che la precedente uguaglianza sia soddisfatta e che \mathbf{s} sia piccolo, quello di firma è più sfidante. Per trovare un generico elemento in \mathbb{Z}_q^k che soddisfi l’equazione è sufficiente ricorrere all’algebra lineare mentre per il requisito sulle dimensioni è necessario utilizzare l’informazione segreta inclusa nella matrice \mathbf{B} e operare con il reticolo da essa generato.
Falcon come istanza di GPV
Considerando gli elementi matematici caratterizzanti del problema \text{NTRU}, Falcon consiste nell’istanziare il framework GPV con i seguenti parametri
\begin{align*}
\mathbf{A}&=\begin{bmatrix}1&h^{\star}\end{bmatrix}\in\mathbb{Z}_q^{n\times2n},\\
\mathbf{B}&=\begin{bmatrix}g&-f\\G&-F\end{bmatrix}\in\mathbb{Z}_q^{2n\times2n},
\end{align*}
ove h^{\star}=h_0+h_{n-1}X+h_{n-2}X^2+\cdots+h_1X^{n-1} e si può verificare che[3].
\mathbf{BA}^{\star}= \begin{bmatrix}g&-f\\G&-F\end{bmatrix}\begin{bmatrix}1\\h\end{bmatrix} = \mathbf{0}\mod q.
La firma di un messaggio m consiste di un sale r e di una coppia di polinomi (s_1,s_2)[4] tali che s_1+s_2h=\text{H}(r||m), ove come \text{H} è utilizzata SHAKE-256.
La randomizzazione con il sale r è introdotta per questioni di sicurezza, infatti la pubblicazione di due firme differenti per lo stesso hash \text{H}(m) vanificherebbe le dimostrazioni di robustezza sottostanti il framework GPV. Il meccanismo di campionamento di (s_1,s_2) prende il nome di Fast Fourier Sampling ed è un particolare esempio di quello che in letteratura viene chiamato trapdoor sampling. Per un’adeguata trattazione si rimanda alla documentazione di Falcon[5].
Si osserva, inoltre, che la particolare forma del primo
q=c\cdot 2n+1,
per un’opportuna costante c, abilita l’utilizzo della Number Theoretic Trasform (NTT) consentendo di ottimizzare agevolmente le operazioni fra polinomi a coefficienti interi. Nello specifico, la NTT, presente anche nel meccanismo di incapsulamento chiave Kyber selezionato dal NIST e in Dilithium, semplifica notevolmente l’operazione di moltiplicazione.
Performance
Fra i candidati del processo di standardizzazione del NIST, Falcon è quello che ha proposto una soluzione ottimale (quindi minimale) in termini di dimensione della coppia chiave pubblica-firma, comunicata unitamente a ciascun messaggio. Minimizzare la dimensione di questi due elementi è quindi cruciale per non impattare eccessivamente sui costi di trasmissione dello schema.
Come si evince dal seguente istogramma, Falcon vanta anche una certa efficienza negli algoritmi di firma e verifica. D’altra parte, la fase di generazione chiavi risulta meno brillante, almeno nel confronto con Dilithium.
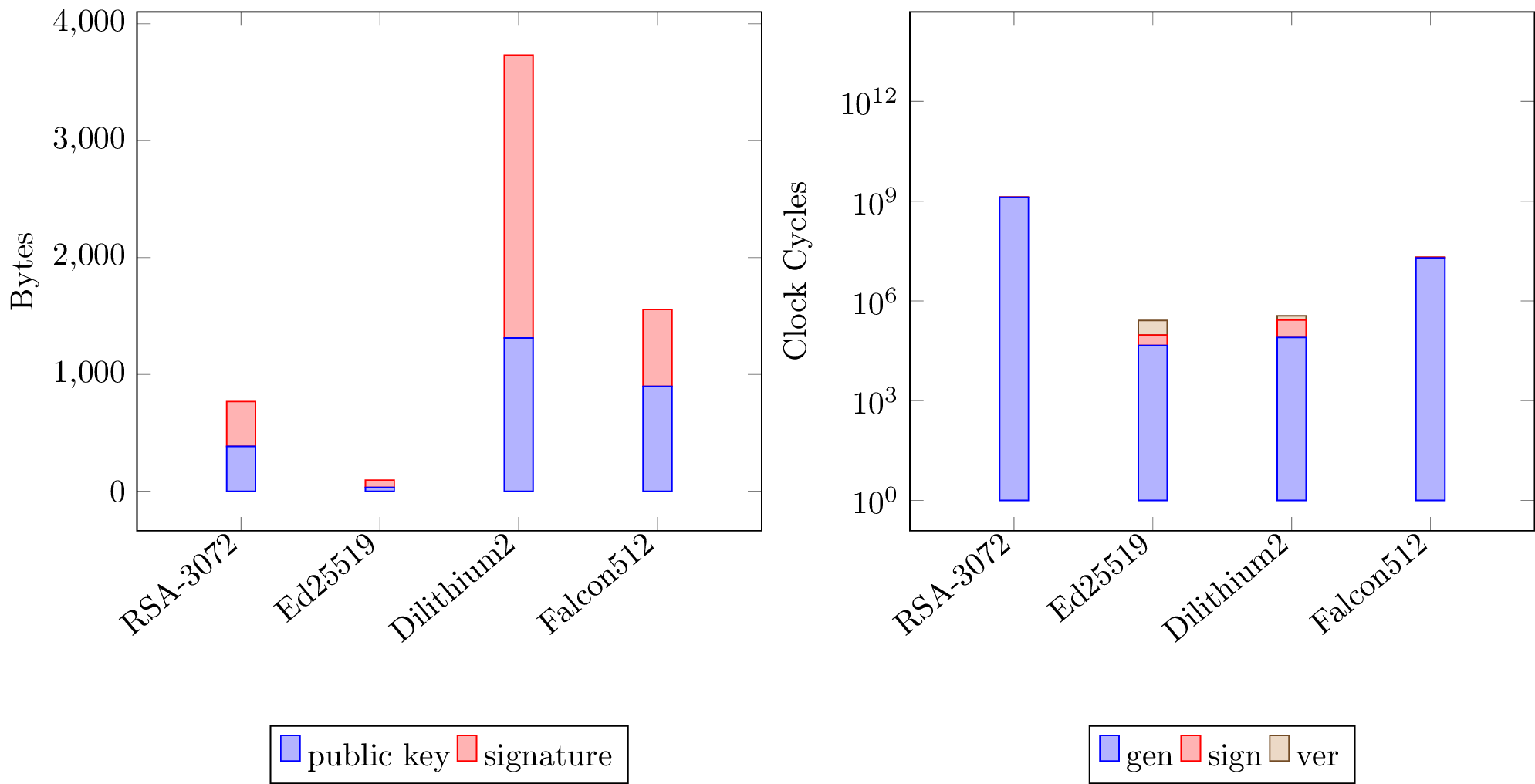
Inoltre, in una valutazione di utilizzo RAM, Falcon è molto più oneroso di Dilithium impattando eventuali implementazioni su dispositivi di tipo constrained come smart cards.
Infine, ulteriore considerazione, che rende l’implementazione sicura di Falcon non banale, è la necessità del coinvolgimento di aritmetica floating point. Infatti, per utilizzare la tecnica Fast Fourier sampling non è possibile limitarsi a considerare numeri interi e l’esecuzione/protezione di operazioni fra numeri reali è sfidante, soprattutto a livello hardware.
[1] polinomi a coefficienti di dimensioni contenute
[2] noto anche come hash-then-sign
[3] per il passaggio dalla nozione di trasposta \cdot^T a quella di aggiunta \cdot^\star si fa riferimento alla documentazione di Falcon [5]
[4] ai fini di ottimizzare la dimensione della firma, sono trasmessi solo r e s_2 visto che s_1 è facilmente determinato di conseguenza
[5] P. Foque, J. Hoffstein, P. Kirchner, V. Lyubashevsky, T. Pornin, T. Prest, G. Seiler, W. Whyte e Z. Zhang. FALCON: Fast-Fourier Lattice-based Compact Signatures over NTRU. 2020
Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.
Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.
L’autore
Francesco Stocco, laureato magistrale in Matematica presso l’Università degli Studi di Padova e l’Université de Bordeaux frequentando il percorso di studi “Algebra Geometry And Number Theory” (ALGANT), entrato a far parte del Gruppo di Ricerca in Crittografia di Telsy alla fine del 2020.
