CRYSTALS-Kyber: incapsulamento chiave basato su LWE
Nel contesto del processo di standardizzazione del NIST per l’individuazione e l’analisi di soluzioni di Post-Quantum Cryptography (PQC), il primo esito cruciale è rappresentato dalla selezione del meccanismo di incapsulamento chiave (KEM) CRYSTALS-Kyber.
Kyber è uno schema crittografico a chiave pubblica che consente a due parti di derivare un segreto comune con cui proteggere lo scambio di informazione.
Le principali caratteristiche, che hanno consentito a Kyber di essere selezionato come soluzione primaria nell’ambito dei KEM fra le 45 proposte NIST iniziali, vanno ricercate nell’efficienza e nella sicurezza garantita di fronte ai migliori attacchi classici e quantistici noti in letteratura.
All’interno degli attuali protocolli crittografici, Kyber andrà a sostituire le tecniche di scambio chiave crittografiche basate su problemi vulnerabili al quantum computing come il diffusissimo ECDH, scambio chiave Diffie Hellman costruito su curve ellittiche.
CRYSTALS-Kyber
Ai fini di comprendere il razionale dietro al design di Kyber, è opportuno procedere per passi.
Il punto di partenza è lo schema di cifratura basato su LWE , il secondo passo è un’estensione a Module-LWE mentre l’ultimo è una trasformazione da schema di cifratura a meccanismo di incapsulamento chiave.
Prima di affrontare la trattazione, è utile fissare alcune notazioni.
- q è un numero primo
- \mathbb{Z}_q indica l’insieme \{0,\dots,q-1\}
- R_q=\mathbb{Z}_q[X]/(X^n+1) indica l’insieme dei polinomi in X a coefficienti in \mathbb{Z}_q con relazione X^n=-1
- Sia S un insieme, s\leftarrow S indica che s è campionato uniformemente in S
- s\in S\gets B_{\eta} indica che s è campionato dalla distribuzione binomiale centrata [1] di parametro \eta
- f\in R_q\gets B_\eta indica che ciascun coefficiente di f è campionato da B_\eta
- \textsf{H}, \textsf{G} sono funzioni di hash
- \textsf{KDF} è una funzione di key derivation
LWE Public Key Encryption (PKE)
Come accade per un generico schema di cifratura a chiave pubblica, LWE PKE si compone di tre algoritmi: generazione delle chiavi, cifratura e decifratura. Si osserva come LWE PKE sia di fatto uno schema “giocattolo” in quanto permette la cifratura di un singolo bit x\in\{0,1\}.
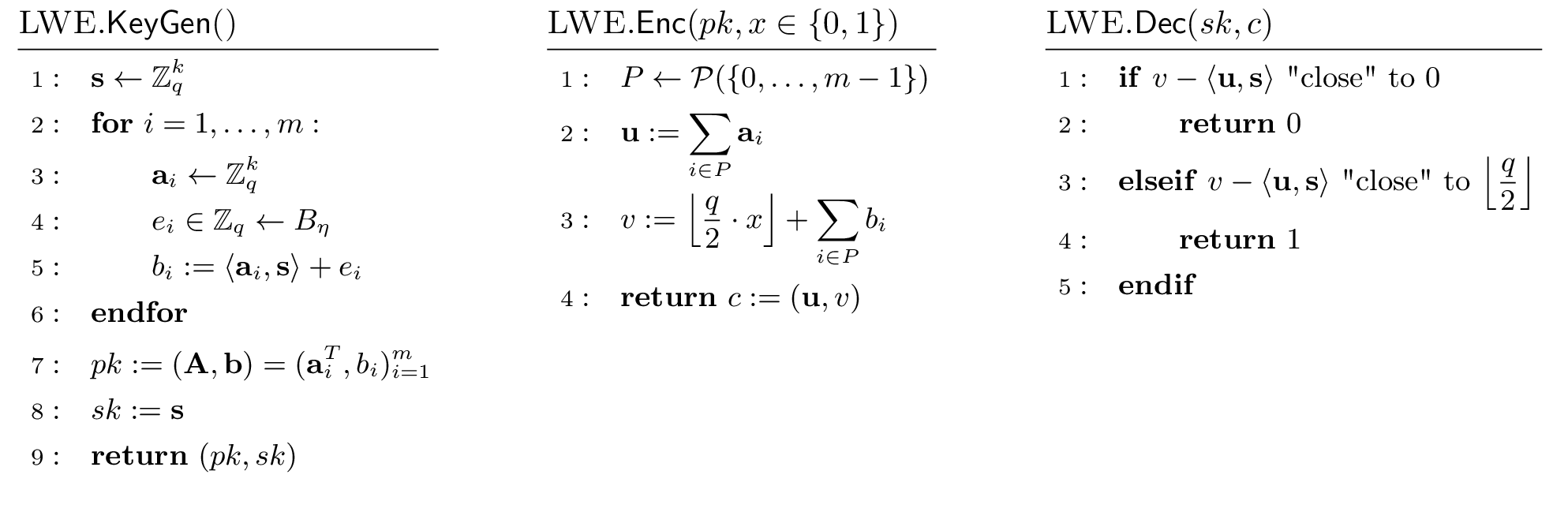
- Generazione chiavi : il vettore \mathbf{s} e la matrice \mathbf{A} sono campionati uniformemente in \mathbb{Z}_q^k e \mathbb{Z}_q^{m\times k} rispettivamente. L’errore \mathbf{e}=(e_1,\dots,e_m)^{T}\in\mathbb{Z}_q^{m} è campionato secondo la distribuzione B_\eta^m. \mathbf{s} costituisce la chiave privata mentre la coppia (\mathbf{A},\mathbf{b}=\mathbf{As}+\mathbf{e}) la chiave pubblica. Si osservi che per questioni di sicurezza m > k.
- Cifratura di x\in\{0,1\}: il cifrato è costituito da un vettore \mathbf{u}\in\mathbb{Z}_q^k ottenuto dalla somma delle righe di \mathbf{A} corrispondenti ad un certo sottoinsieme di indici P e da un elemento v\in\mathbb{Z}_q risultato della somma delle entrate di \mathbf{b} corrispondenti a P e del valore \lfloor \frac{q}{2} \cdot x\rfloor [2]. Si osservi che se un attaccante intercetta P può risalire direttamente al messaggio x, pertanto il campionamento uniforme di P risulta fondamentale.
- Decifratura di (\mathbf{u},v): grazie alla conoscenza della chiave privata, x è riottenuto valutando se il valore v-\langle \mathbf{u}, \mathbf{s}\rangle è più vicino a 0 o a \lfloor \frac{q}{2}\rfloor.
Kyber Public Key Encryption (PKE)
Lo schema Kyber PKE mima il caso sopra discusso con una variazione nella struttura matematica in cui vivono gli elementi considerati, infatti si passa da \mathbb{Z}_q a R_q.
È bene osservare come Kyber PKE, nonostante non sia una costruzione giocattolo, non possa comunque essere utilizzato come soluzione di cifratura “standalone” in quanto non garantisce tutti i requisiti di sicurezza necessari in un contesto pratico. Infatti, questa costruzione realizza una sicurezza di tipo IND-CPA [3] ( indistiguishability under chosen plaintext attack ), un livello di sicurezza standard in crittografia ma insufficiente nella maggior parte dei casi d’uso.
Il ruolo fondamentale di Kyber PKE è piuttosto quello di fungere da building block per il meccanismo di incapsulamento chiave esposto da Kyber.

Ad alto livello, i passaggi sono i medesimi di LWE PKE.
- Generazione chiavi : il vettore segreto \mathbf{s}\in R_q^k e l’errore \mathbf{e}\in R_q^k sono campionati secondo le distribuzioni B_{\eta_1}^k e B_{\eta_2}^k rispettivamente. La matrice pubblica \mathbf{A} è campionata uniformemente in R_q^{k\times k}.
- Cifratura di m\in R_q: il vettore \mathbf{r}\in R_q^k, campionato da B_{\eta_1}^k, ha lo stesso ruolo di P nel caso LWE PKE. Il campionamento aggiuntivo degli errori \mathbf{e}_1\in R_q^k ed e_2\in R_q è necessario per questioni di sicurezza, in quanto, a differenza di LWE PKE, si lavora con la matrice \mathbf{A} quadrata [4]. Il simbolo \lceil\cdot\rfloor indica che si sta calcolando per ciascun coefficiente dell’elemento considerato l’approssimazione all’intero più vicino.
- Decifratura di (\mathbf{u},v): la ratio che guida la decifratura è identica al caso LWE PKE.
La correttezza[5] dello schema è garantita dalla seguente relazione
v-\langle \mathbf{u},\mathbf{s} \rangle= \mathbf{s}^{T}\mathbf{A}^{T}\mathbf{r}+\mathbf{e}^{T}\mathbf{r}+e_2+\Big\lceil\frac{q}{2}\cdot m\Big\rfloor-\mathbf{s}^{T}\mathbf{A}^{T}\mathbf{r}-\mathbf{s}^{T}\mathbf{e_1}= \Big\lceil\frac{q}{2}\cdot m\Big\rfloor + \underbrace{\mathbf{e}^{T}\mathbf{r} -\mathbf{s}^{T}\mathbf{e_1}+e_2}_{\text{termini di errore}}.
Fujisaki-Okamoto Transform (FO)
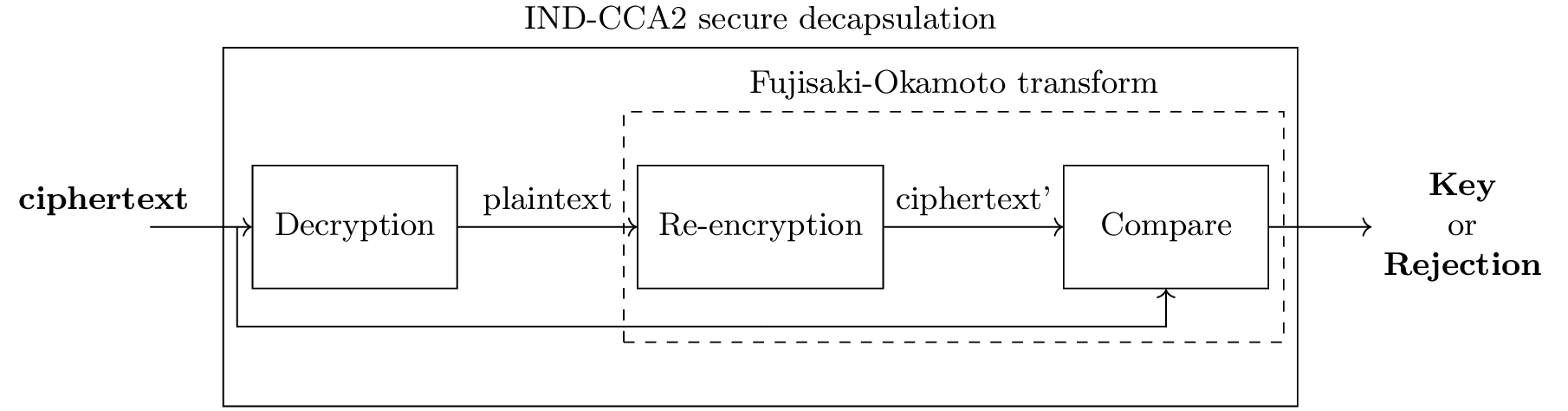
L’ultimo passaggio per la costruzione del meccanismo di incapsulamento chiave proposto da Kyber è l’applicazione di una variante della trasformazione Fujisaki-Okamoto. Questa operazione, nota in letteratura, consente di realizzare uno schema KEM con sicurezza IND-CCA2 a partire da uno schema PKE con sicurezza IND-CPA.
Il livello IND-CCA2 [3] ( indistinguishability under adaptive chosen ciphertext attack ) è un tipo di sicurezza standard in crittografia che, a differenza del più debole IND-CPA, è adatto a contesti applicativi reali.
L’azione più rilevante della trasformazione FO si nota in fase di ricezione di un ciphertext.
Una volta decifrato un ciphertext, il plaintext corrispondente viene ricifrato e confrontato con quello ricevuto. Lo scopo è di aggiungere un livello di validazione dell’informazione.
Qualora la comparazione abbia esito positivo, una chiave crittografica viene derivata, altrimenti il ciphertext viene ritenuto invalido e rifiutato.
Kyber Key Encapsulation Mechanism (KEM)

Gli algoritmi di generazione chiavi, incaspulamento e decapsulamento di Kyber poggiano su generazione chiavi, cifratura e decifratura di Kyber PKE.
- Generazione chiavi : l’algoritmo è sostanzialmente il medesimo di Kyber PKE. La distinzione più rilevante risiede nel campionamento di un segreto aggiuntivo z che entra in gioco in caso di rifiuto in fase di decapsulamento.
- Incapsulamento : un plaintext m è campionato uniformemente. La chiave condivisa K è ottenuta a partire da m e dal cifrato c corrispondente.
- Decapsulamento di c: le fasi della trasformazione FO descritta in precedenza sono evidenziate in rosso . Si osserva una particolarità del meccanismo di rifiuto: nel caso in cui il decapsulamento non dia esito positivo non viene restituito un messaggio d’errore ma una chiave random a partire dal segreto z campionato in precendenza. In questa eventualità, le due parti sono in possesso di due chiavi crittografiche distinte e la discrepanza viene rilevata solo in una fase di comunicazione successiva, si parla infatti di implicit rejection . La ratio dietro a questa strategia riguarda una maggior resistenza a cattivi utilizzi. Ad esempio, si vuole evitare che, in mancanza di verifica dell’esito del decapsulamento, alla richiesta di chiave crittografica venga comunque fornita una stringa di default a bassa entropia.
Performance in software
Analizzando le performance dello schema in software, si realizza che l’onere computazionale è suddiviso secondo il seguente grafico a torta [6].
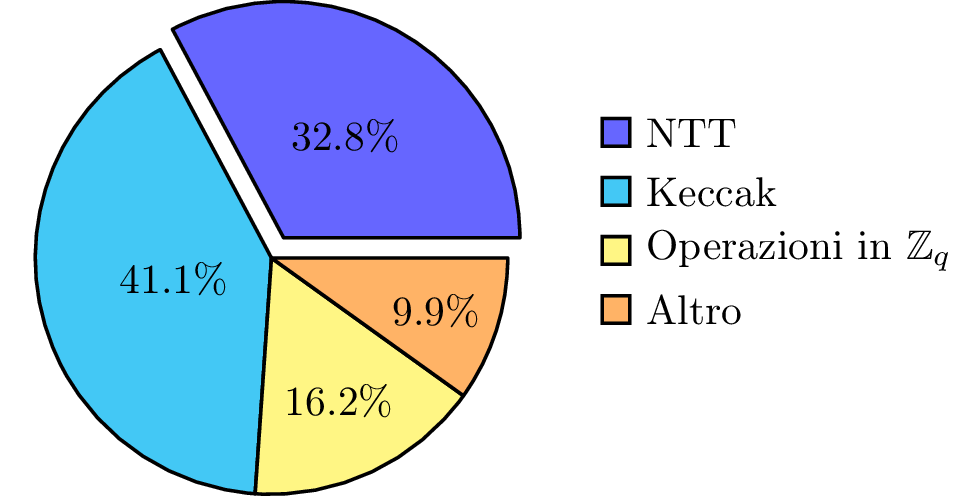
La dicitura Keccak , che risulta la parte più intesiva, raggruppa tutte le primitive simmetriche [7] riportate di seguito.
| \textsf{H} | SHA3-256 |
| \textsf{G} | SHA3-512 |
| \textsf{KDF} | SHAKE-256 |
| \textsf{XOF}[8] | SHAKE-128 |
| \textsf{PRF}[8] | SHAKE-256 |
La NTT[9], invece, indica una particolare trasformazione di elementi in R_q ed è denotata come
f = f_0 + f_1\cdot X + \cdots f_{n-1}\cdot +X^{n-1}\xmapsto[]{\textsf{NTT}} \hat{f} = \hat{f}_0 + \hat{f}_1\cdot X + \cdots +\hat{f}_{n-1}\cdot X^{n-1}.
Grazie alla NTT il prodotto di due elementi f e g è dato da
fg = \textsf{NTT}^{-1}(\hat{f}\circ\hat{g}),
ove \hat{f}\circ\hat{g} è calcolato componente per componente
(\hat{f}\circ\hat{g})_i=\hat{f}_i\cdot \hat{g}_i,
risultando molto efficiente dal punto di vista computazionale.
Nel contesto della standardizzazione post-quantum del NIST, l’efficienza computazionale ha giocato un ruolo fondamentale. In questa direzione, punto di forza di Kyber è rappresentato proprio dall’efficientamento delle moltiplicazioni fra elementi in R_q garantito dall’applicazione della NTT.
[1] Campionamento da B_{\eta}: \begin{align*} &\{(a_i,b_i)\}^{\eta}_{i=1} \longleftarrow (\{0,1\}^2)^\eta\\\text{output } & \sum_{i=1}^{\eta}(a_i-b_i)\in\{-\eta\dots,-1,0,1\dots,\eta\}.\end{align*}
[2] \lfloor\cdot\rfloor indica la parte intera.
[3] pagina Wikipedia
[4] Qualora \mathbf{e_1}, e_2 fossero nulli e \mathbf{A} di rango massimo, da \mathbf{u} si potrebbe ricavare \mathbf{r} e successivamente da v si potrebbe dedurre il messaggio m.
[5] Lo schema è corretto se vale \text{Kyber}.\textsf{CPAPKE}.\textsf{Dec}(sk,\text{Kyber}.\textsf{CPAPKE}.\textsf{Enc}(pk,m))=m.
[6] performance dell’implementazione di riferimento di Kyber in un processore Intel Core i7-8665U
[7] scelte secondo lo standard FIPS-202
[8] \textsf{XOF} e \textsf{PRF} non sono trattate in questo articolo, intervengono nei passaggi di campionamento.
[9] Si precisa come la NTT implementata in Kyber sia una lieve variazione di quella qui presentata a scopo divulgativo.
Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.
Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.
Gli autori
Veronica Cristiano, laureata triennale in Matematica presso l’Università di Pisa e laureata magistrale in Matematica con specializzazione in Crittografia presso l’Università di Trento, entrata a far parte del gruppo di ricerca in Crittografia di Telsy a metà del 2021.
Francesco Stocco, laureato magistrale in Matematica presso l’Università degli Studi di Padova e l’Université de Bordeaux frequentando il percorso di studi “Algebra Geometry And Number Theory” (ALGANT), entrato a far parte del gruppo di ricerca in Crittografia di Telsy alla fine del 2020 occupandosi in particolare di temi inerenti alle tecnologie quantistiche.

