L’Algoritmo Quantistico di Grover
Introduzione
Con l’articolo del 1996 “A fast quantum mechanical algorithm for database search”, l’informatico indiano-americano Lov K. Grover ha contribuito a mettere in evidenza l’impatto non trascurabile del quantum computing sulla crittografia oggi in uso.
Il lavoro di Grover riguarda il metodo di ricerca in un database non strutturato, quindi privo di qualsiasi ordinamento che faciliti l’operazione.
Per comprendere il contributo dell’algoritmo di Grover, si riporta un semplice esempio. Si consideri un comune elenco telefonico in cui compaiono i nomi ordinati in ordine alfabetico e accanto a ciascuno il corrispondente numero di telefono.
Si supponga, però, di dover effettuare una ricerca inversa rispetto alla consuetudine e, quindi, di avere un certo numero di telefono di cui si vuole identificare il proprietario.
Quello che un approccio classico prevede per risolvere tale problema è scorrere l’elenco e controllare i numeri uno ad uno fino a trovare quello desiderato, identificando il nome associato.
Quindi, nel caso peggiore, per individuare il nominativo è necessario controllare tutti i numeri contenuti nell’elenco tranne l’ultimo.
Invece, attraverso l’algoritmo di Grover, un computer quantistico risolverebbe la stessa istanza in un numero di “controlli quantistici” molto minore rispetto al caso classico. In particolare, si parla di speed up quadratico rispetto al caso classico.
Questo significa che, dato un problema di ricerca, se nel caso classico questo richiede un numero N di controlli, nel caso quantistico, con l’algoritmo di Grover, sono sufficienti circa \sqrt{N} controlli quantistici.
Tornando all’esempio precedente, se l’elenco telefonico fosse composto da 10000 contatti, l’approccio classico richiederebbe 9999 controlli nel caso peggiore, mentre l’approccio quantistico si limiterebbe a meno di 100.
Qualora un computer quantistico con adeguate caratteristiche venisse realizzato, le implicazioni di sicurezza più rilevanti del risultato di Grover si riscontrerebbero nella crittografia simmetrica oggi in uso.
Ad esempio, si consideri lo schema di cifratura AES (Advanced Encrytption Standard) con chiave crittografica k di lunghezza 128 bit e si assuma che un attaccante conosca alcune coppie testo in chiaro-testo cifrato e che voglia trovare la chiave con cui, per ciascuna delle coppie conosciute, a partire dal testo in chiaro si ottiene il testo cifrato corrispondente e viceversa.
Allo stato dell’arte non è noto un attacco che operi in maniera significativamente migliore di una ricerca esaustiva per individuare la chiave[1].
Nel caso classico, la ricerca esaustiva richiederebbe circa 2^{128} chiamate all’oracolo[2] O per stabilire k mentre, nel caso quantistico, l’algoritmo di Grover invocherebbe l’oracolo U circa 2^{64} volte con probabilità di successo molto vicina ad 1.
Spesso accade che nella narrativa corrente l’algoritmo di ricerca ideato da Grover venga descritto come uno strumento che “dimezza” la sicurezza della crittografia simmetrica oggi in uso.
Questo dimezzamento è relativo alla lunghezza in bit della chiave coinvolta, ad esempio rompere AES con chiave da 128 bit attraverso l’algoritmo di Grover necessita un numero di invocazioni all’oracolo quantistico paragonabile al numero di invocazioni all’oracolo classico per rompere AES con chiave da 64 bit, attraverso la ricerca esaustiva.
Di conseguenza, è plausibile aspettarsi che per ripristinare la sicurezza degli schemi simmetrici, alla luce degli sviluppi del quantum computing, sia sufficiente raddoppiare la dimensione in bit delle chiavi crittografiche.
Tuttavia, si tratterebbe di una scelta particolarmente conservativa nella pratica, in quanto il dimezzamento della sicurezza può considerarsi effettivo solo in parte almeno per due motivazioni.
La prima ragione è la difficoltà nello stabilire in modo preciso il costo computazionale dell’esecuzione di U, che comunque si ritiene superiore a quello di O[3].
Il secondo aspetto da tenere in considerazione è l’impossibilità di parallelizzare in modo efficiente l’algoritmo quantistico di ricerca, che quindi sarebbe genericamente eseguito in un unico processore quantistico, mentre l’onere computazionale della ricerca esaustiva può essere suddiviso fra più dispositivi che operano in modo parallelo.
Le seguenti sezioni sono dedicate ad una descrizione tecnica dell’algoritmo e del circuito quantistico ideato da Grover. Per comprendere a pieno la trattazione, si consiglia di riprendere i concetti introdotti nell’articolo precedente.
Qubit come vettori
Al fine di interpretare il razionale su cui è basato il lavoro di Grover, è opportuno rivedere la definizione dei qubit in termini vettoriali.
Sia lo spazio vettoriale n-dimensionale \mathbb{C}^n dotato del prodotto scalare usuale sui numeri complessi, ciascun n-qubit è associato ad un vettore di norma 1 in questo spazio.
In particolare, i vettori corrispondenti ai qubit della forma |x_0\cdots x_{n-1}\rangle sono detti di base.
A titolo esemplificativo, si riportano i casi n=1 ed n=2. Per n=1: \begin{aligned} \text{1-qubit di base: } | & 0\rangle \longleftrightarrow \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \qquad |1\rangle \longleftrightarrow \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \\ \text{1-qubit generico: } | & \psi\rangle = \alpha |0\rangle + \beta |1\rangle \longleftrightarrow \begin{pmatrix} \alpha \\ \beta \end{pmatrix}. \end{aligned} Per n=2: \begin{aligned} \text{2-qubit di base: }| & 00\rangle \longleftrightarrow \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}, \qquad |01\rangle \longleftrightarrow \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}, \qquad |10\rangle \longleftrightarrow \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}, \qquad |11\rangle \longleftrightarrow \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}, \\ \text{2-qubit generico: }| & \psi\rangle = \alpha |00\rangle + \beta |01\rangle +\gamma |10\rangle + \delta |11\rangle\longleftrightarrow \begin{pmatrix} \alpha \\ \beta \\ \gamma \\ \delta \end{pmatrix}. \end{aligned}
Circuito di Grover
In una formulazione numerica dell’algoritmo di ricerca di Grover, senza perdita di generalità, si può pensare di effettuare la ricerca nell’insieme dei primi N numeri naturali con N=2^n, che nella loro rappresentazione binaria sono:\begin{aligned} 0 & \leftrightarrow 0\dots 000 \\ 1 & \leftrightarrow 0\dots 001 \\ 2 & \leftrightarrow 0\dots 010 \\ \vdots & \\ N-1 & \leftrightarrow \underbrace{1\dots 111}_{n} \end{aligned} Il fatto che solo un particolare a\in\{0,1\}^n soddisfi una certa condizione è identificabile dalla definizione della seguente funzione f che risponde 1 se l’input è a e 0 in tutti gli altri casi.\begin{aligned} f\colon \{0,1\}^n & \longrightarrow \{0,1\} \\ a & \longmapsto 1 \\ x (\neq a) & \longmapsto 0 \end{aligned}
Si assume di avere accesso alla funzione tramite l’oracolo O_f, ovvero f non è nota ma dato x\in\{0,1\}^n è possibile ottenere la valutazione f(x).
In assenza di ulteriori informazioni in merito alla disposizione degli interi compresi fra 0 e N-1 rispetto a f, un computer classico non può far altro che procedere con una ricerca esaustiva ed applicare l’oracolo a differenti elementi in \{0,1\}^n fino all’individuazione di a.
Per avere una probabilità di successo di \frac{m}{N} è necessario chiamare l’oracolo su m interi distinti.
In particolare, una probabilità di individuare a maggiore di \frac{1}{2} è ottenibile effettuando almeno \frac{N}{2} chiamate all’oracolo mentre, nel caso peggiore, per una risposta deterministica le invocazioni all’oracolo sono N-1.
Essendo lineare in N, il numero di chiamate all’oracolo è denotato con O(N) in termini asintotici.
Con le stesse ipotesi sul database, il lavoro di Grover del 1996 propone un algoritmo quantistico in grado di risolvere il problema di ricerca con probabilità molto vicina a 1 ma con un numero di chiamate all’oracolo quantistico U_f vicino a \frac{\pi}{4}\sqrt{N} per N grande, asintoticamente O(\sqrt{N}).
Essendo coinvolto un numero di chiamate lineare in \sqrt{N}, si parla di speed-up quadratico rispetto all’algoritmo classico di ricerca esaustiva.
Più nel dettaglio, si ricordi l’applicazione di U_f ad un registro di n+1 qubit. U_f(|x_0\cdots x_{n-1}\rangle |y\rangle) = |x_0\cdots x_{n-1}\rangle |y\oplus f(x_0\cdots x_{n-1})\rangle Data la funzione f definita come sopra, si osservi l’applicazione di U_f all’n+1-qubit |x\rangle H |1\rangle[4], ove x=x_0\cdots x_{n-1}. U_f(|x\rangle H|1\rangle)=|x\rangle(-1)^{f(x)}H|1\rangle = (-1)^{f(x)}|x\rangle H |1\rangle In questa forma, si può interpretare U_f come un gate V_f che agisce solo sui primi n-qubit come V_f|x\rangle = (-1)^{f(x)}|x\rangle = \begin{cases} |x\rangle \text{ se } x\neq a,\\ -|a\rangle \text{ se } x = a. \end{cases}
Dato un generico n-qubit, V_f cambia il segno della componente lungo |a\rangle mentre lascia invariata quella ortogonale a |a\rangle.
Data la superposizione uniforme[5] |\phi\rangle = \underbrace{H|0\rangle \cdots H|0\rangle}_{n}= \frac{1}{2^{\frac{n}{2}}}\sum_{x=0}^{2^n-1}|x\rangle, si definisce, in modo simile a V_f, la trasformazione W che agisce su un generico n-qubit fissando la componente lungo |\phi\rangle e cambiando di segno quella ortogonale a |\phi\rangle. La ripetuta applicazione in successione delle trasformazioni V_f e W allo stato |\phi\rangle permette all’algoritmo di Grover di determinare |a\rangle in O(\sqrt{N}) passi.
Di seguito si riporta il dettaglio del circuito corrispondente e la dimostrazione di correttezza.
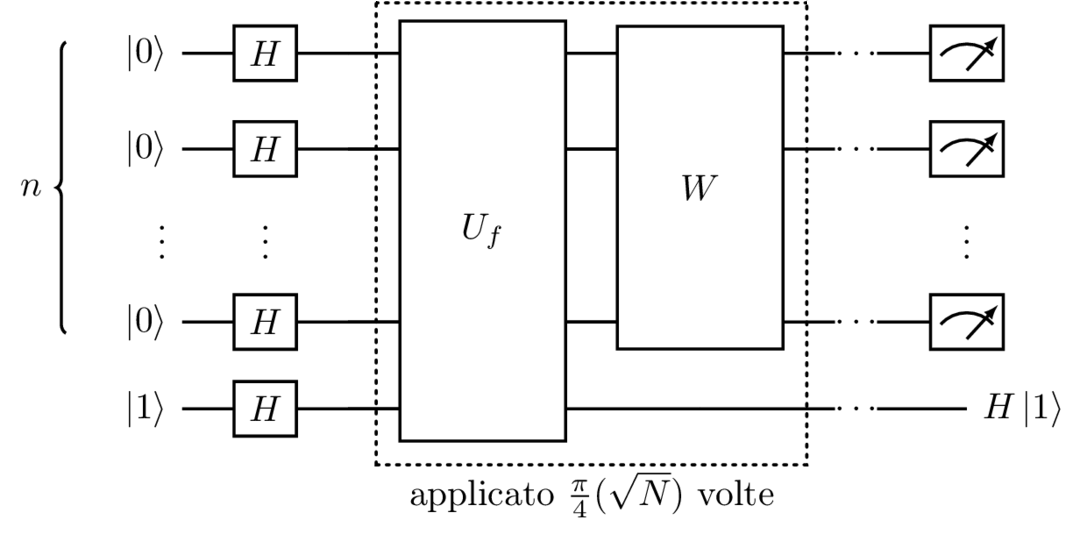
Il primo passaggio consiste nell’applicazione del gate di Hadamard H allo stato |0\cdots01\rangle. Questo consente di porre i primi n qubit nella superposizione uniforme |\phi\rangle e ignorare successivamente l’ultimo qubit considerandolo come ausiliario al calcolo, vista la precedente osservazione su V_f.
A seguire, siccome l’azione di V_f e W sugli stati |\psi\rangle e |a\rangle restituisce combinazioni lineari a coefficienti reali di questi due stati \begin{aligned} & V_f|a\rangle=-|a\rangle, & & V_f|\phi\rangle=|\phi\rangle-\frac{2}{2^{\frac{n}{2}}}|a\rangle, \\\ & W|a\rangle = \frac{2}{2^{\frac{n}{2}}}|\phi\rangle-|a\rangle, & & W|\phi\rangle=|\phi\rangle, \end{aligned} si può restringere l’analisi al piano reale generato da |\phi\rangle e |a\rangle.
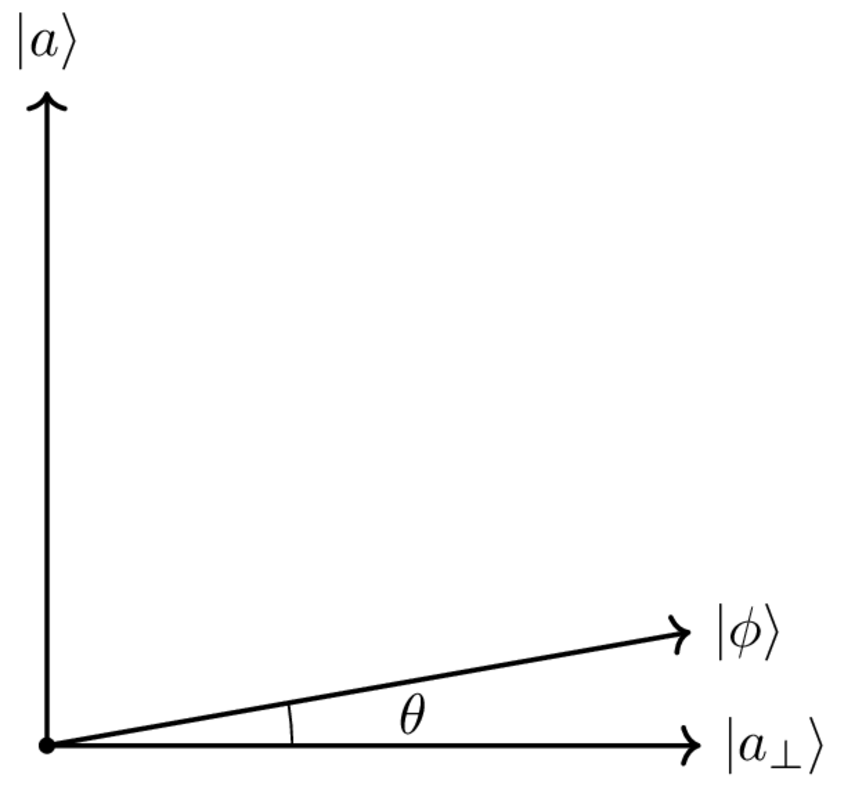
Nel piano individuato V_f si riduce ad una simmetria rispetto a |a_{\bot}\rangle, ove |a_{\bot}\rangle è l’ortogonale a |a\rangle “vicino” a |\phi\rangle, mentre W ad una simmetria rispetto a |\phi\rangle.
Per N abbastanza grande , possiamo approssimare l’angolo \theta fra |a_{\bot}\rangle e |\phi\rangle con \sin\theta, infatti[6] \sin\theta=\cos\Big(\frac{\pi}{2}-\theta\Big)=\langle a|\phi \rangle = \frac{1}{2^{\frac{n}{2}}}=\frac{1}{\sqrt{N}}\implies \theta\approx\frac{1}{\sqrt{N}}.
La combinazione delle simmetrie V_f e W risulta in una rotazione di tutti i qubit del piano descritto di angolo 2\theta in direzione antioraria.
In particolare, l’immagine descrive l’azione sul qubit |\phi\rangle.
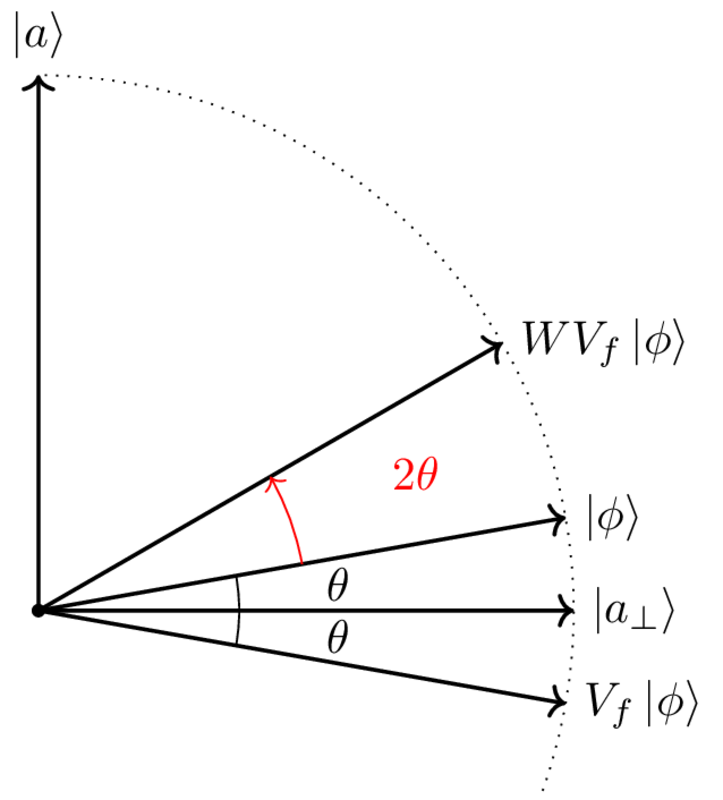
Ripetendo questa operazione k volte, in modo da percorrere tutto l’arco da |\phi\rangle a |a\rangle, si ottiene uno stato quantistico che una volta misurato collasserà ad |a\rangle con probabilità molto vicina ad 1.
Per completezza, k è ottenuto risolvendo l’equazione \frac{2\pi}{2\theta}=2k+1, da cui k risulta l’intero più vicino al numero reale \frac{\pi}{4}\sqrt{N}.
[1] Il miglior attacco noto contro AES è il Biclique che fa guadagnare circa un fattore 4 rispetto alla ricerca esaustiva
[2] L’oracolo di una funzione f è uno strumento che consente di ottenere la valutazione di f su un dato input senza conoscere nel dettaglio la definizione di f. In questo caso l’oracolo risponde affermativamente se e solo se la chiave è quella giusta. Si denota con O l’oracolo classico, con U l’oracolo quantistico
[3] Si osservi che l’effettivo costo totale è dato dal prodotto tra il numero di esecuzioni dell’oracolo e il costo di una singola esecuzione dello stesso
[4] Si ricorda H|0\rangle=\big(\frac{1}{\sqrt{2}} |0\rangle +\frac{1}{\sqrt{2}}|1\rangle\big), H|1\rangle=\big(\frac{1}{\sqrt{2}} |0\rangle -\frac{1}{\sqrt{2}}|1\rangle\big)
[5] Superposizione fra tutti i qubit di base considerati con lo stesso coefficiente reale e, quindi, con la stessa probabilità
[6] Si noti che la scrittura \langle a|\phi \rangle indica il prodotto scalare fra |a\rangle e |\phi\rangle
Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.
Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.
Gli autori
Veronica Cristiano, laureata triennale in Matematica presso l’Università di Pisa e laureata magistrale in Matematica con specializzazione in Crittografia presso l’Università di Trento, entrata a far parte del gruppo di ricerca in Crittografia di Telsy a metà del 2021.
Francesco Stocco, laureato magistrale in Matematica presso l’Università degli Studi di Padova e l’Université de Bordeaux frequentando il percorso di studi “Algebra Geometry And Number Theory” (ALGANT), entrato a far parte del gruppo di ricerca in Crittografia di Telsy alla fine del 2020 occupandosi in particolare di temi inerenti alle tecnologie quantistiche.
