Il Quantum Computing
La storia del quantum computing
Alla fine dello scorso secolo, il campo della fisica sperimentale è stato rivoluzionato dallo sviluppo tecnologico dei computer classici. Fra le numerose innovazioni, la possibilità di simulare al computer il comportamento di particelle subatomiche ha favorito la comprensione della natura di alcuni fenomeni fisici da parte degli scienziati.
Nonostante l’impatto promettente dei nuovi sistemi di elaborazione, è risultato evidente che le limitazioni di calcolo dei computer avrebbero consentito la simulazione di sistemi fisici di complessità contenute. In effetti, il costo computazionale per la riproduzione fedele di un sistema cresce in modo esponenziale all’aumentare delle particelle coinvolte.
La teorizzazione originaria del computer quantistico, storicamente attribuita al premio Nobel per la fisica Richard Feynman impegnato nello studio della materia e dei fenomeni naturali, si colloca precisamente in questo contesto.
In seguito a delle discussioni avute con il fisico digitale Edward Friedkin, Feynman si convinse che la risposta alle esigenze di calcolo sopra identificate andasse ricercata nelle leggi della meccanica quantistica. Storica è la frase a lui attribuita:
“Nature is quantum, goddamn it! So if we want to simulate it, we need a quantum computer.”
Richard Feynman
Se da un lato si associa alla fisica classica la scienza che affronta lo studio dei fenomeni naturali a livello macroscopico, come la relazione fra massa e forza di gravità, con la meccanica quantistica si identifica la scienza che si occupa di descrivere e comprendere i fenomeni microscopici, come l’interazione fra particelle subatomiche.
Quanto Feynman voleva evidenziare con la sua affermazione è che la fisica e, più in generale, le scienze non possono esimersi dallo studio della natura e quindi della materia partendo dai fenomeni microscopici che la determinano. Pertanto, un computer con l’obiettivo di simulare questi fenomeni deve poter elaborare l’informazione con la stessa logica che li caratterizza.
In effetti, la logica con cui il mondo microscopico evolve è diversa da quella a cui siamo abituati e ci pone di fronte ad eventi che vanno contro l’intuizione comune. Un esempio rappresentativo è il fenomeno della superposizione che, con opportune semplificazioni, si può immaginare in relazione a ciascun evento descrivibile da due o più stati.
Si pensi al lancio di una moneta: il fenomeno della superposizione è interpretabile come la possibilità di considerare combinazioni intermedie fra i due esiti possibili (testa e croce), associabili a tutte le configurazioni della moneta quando sta ruotando.

Di fatto, mentre la moneta è ancora in aria, si sa che una volta caduta a terra assumerà uno dei due valori ma ancora non è evidente quale e, pertanto, si devono tenere in considerazione entrambe le eventualità. Questa sorprendente intuizione è alla base dell’unità di informazione elaborata dai computer quantistici.
In natura, diversi fenomeni microscopici sono descrivibili grazie alla superposizione. Qualora il lettore fosse interessato all’approfondimento, alcuni di questi comportamenti relativi a particelle subatomiche, come la posizione nello spazio, il livello energetico e lo spin, ne sono un esempio.
Per citare un’implicazione medica, il processo fisico che consente di ricavare le immagini nelle odierne risonanze magnetiche nucleari è basato sul porre in superposizione lo spin dei protoni presenti negli atomi d’idrogeno all’interno del nostro corpo.
A partire dalla teorizzazione del computer quantistico proposta da Feynman nel 1982 con l’articolo “Simulating Physics with Computers”, l’idea di utilizzare risorse di calcolo quantistiche si è espansa ad altri campi di applicazione, pur mantenendosi ad un livello teorico.
Grazie alla possibilità di coprire al contempo più configurazioni possibili, i fenomeni quantistici si sono dimostrati straordinariamente vincenti per la modellizzazione e la risoluzione di problemi di combinatoria. Ad esempio, ci si riferisce ad un problema di combinatoria quando dato un insieme di possibili soluzioni si vuole individuare quella ottimale. In questo contesto viene spesso citato il “Travelling Salesman Problem”.
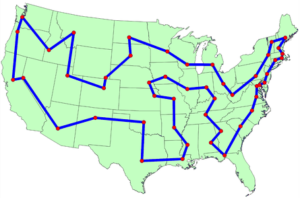
Dati un insieme di città e una lista con la distanza fra ogni coppia di città, con “Travelling Salesman Problem” si definisce il problema di trovare il percorso più breve possibile per recarsi in tutte queste città passandoci una sola volta e tornando al punto di partenza.
Da un punto di vista classico, il costo computazionale per ottenere questo risultato cresce in modo esponenziale all’aumentare del numero di città coinvolte, rendendo la ricerca della soluzione ottimale intrattabile su larga scala. D’altro canto, la capacità combinatoria di un computer quantistico renderebbe questo problema più accessibile.
Telsy e il quantum computing
Visti i recenti sviluppi tecnologici, il gruppo di ricerca di Telsy ha intenzione di occuparsi della realizzazione di una rubrica dedicata alle implicazioni del computer quantistico nell’ambito della crittografia, da sempre elemento cardine nel quadro delle competenze dell’azienda.
L’obiettivo della rubrica sarà quello di fornire le basi per una visione d’insieme dell’ecosistema quantistico ed il presente articolo vuole rappresentarne il punto di partenza.
Di seguito, è fornita una breve introduzione ai temi principali che verranno successivamente sviluppati all’interno della rubrica. Di conseguenza, la terminologia ed alcuni concetti qui presenti non sono trattati in modo esaustivo e verranno ripresi in maggiore dettaglio nei prossimi articoli.
Nell’ambito della crittografia, più precisamente in quello della crittoanalisi, il nuovo modello computazionale ha trovato delle applicazioni estremamente rilevanti. Nel 1995 con l’articolo “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer”, l’informatico teorico Peter Shor ha esposto alla comunità scientifica un algoritmo quantistico in grado di risolvere il problema della fattorizzazione dei numeri interi e del logaritmo discreto in modo esponenzialmente più veloce rispetto alle tecniche classiche.
Il successo riscosso dal lavoro di Shor è determinato dalla minaccia che questo rappresenta per la crittografia asimmetrica (o a chiave pubblica) oggi in uso. In effetti, il protocollo RSA per la cifratura e la firma digitale affonda la propria sicurezza nell’assunzione che il problema della fattorizzazione dei numeri interi sia un problema computazionalmente impossibile da risolvere in tempo ragionevole per un computer classico.
La medesima considerazione vale anche per il protocollo Diffie-Hellmann per lo scambio di chiavi crittografiche, il quale basa la propria sicurezza sull’intrattabilità classica del problema del logaritmo discreto.
Anche la crittografia simmetrica (o a chiave privata) oggi in uso non è risultata immune dall’avvento degli algoritmi quantistici: nel 1996 l’informatico Lov Grover ha teorizzato un algoritmo in grado di trovare la chiave crittografica privata condivisa fra le parti comunicanti, in modo quadraticamente più veloce rispetto alle tecniche classiche.
La minaccia quantum
Se l’impatto sulla crittografia simmetrica non è distruttivo – infatti per proteggersi dall’algoritmo di Grover basta semplicemente raddoppiare la lunghezza della chiave crittografica -, questo non si può dire per la crittografia asimmetrica. Qualora il computer quantistico teorizzato da Feynman venisse effettivamente realizzato, i protocolli RSA e Diffie-Hellman non sarebbero più utilizzabili con adeguate garanzie di sicurezza.

Quantum Computer di IBM
Tale minaccia si è mantenuta ad un livello prettamente teorico almeno fino al primo decennio del nuovo millennio, quando diversi colossi tecnologici come IBM, Google e D-Wave hanno iniziato ad investire sulla realizzazione di un computer quantistico. Lo sforzo di queste compagnie ha portato allo sviluppo di alcuni prototipi di capacità e dimensioni contenute, in termini di potenza di calcolo e memoria.
Nonostante al momento i modelli prototipali abbiano ancora un impatto essenzialmente nullo sulle applicazioni reali, questi rappresentano un punto di partenza incoraggiante per gli sviluppi futuri e consentono alle principali compagnie di ipotizzare percorsi tecnologici più concreti che portino alla realizzazione di un computer quantistico con le medesime potenzialità di quello teorizzato da Feynman. Non è ancora chiaro se e quando questo obiettivo verrà raggiunto e le stime più ottimistiche parlano di almeno una decina d’anni.
In quest’ottica, la comunità crittografica non può farsi trovare impreparata dall’eventualità che nel medio-lungo termine l’algoritmo di Shor possa essere implementato con successo per rompere gli schemi a chiave pubblica oggi in uso.
Inoltre, queste implicazioni rappresentano una criticità che non si può ignorare anche in relazione alla protezione odierna dell’informazione, soprattutto qualora questa necessiti di rimanere confidenziale per lunghi periodi di tempo. Più concretamente, un attaccante interessato ad ottenere informazioni oggi inaccessibili potrebbe limitarsi ad intercettarle cifrate e un domani, con l’evoluzione tecnologica del computer quantistico, decifrarle seguendo quella strategia spesso descritta come “store now, decrypt later”.
La risposta crittografica
La risposta crittografica a questa minaccia si sta muovendo in due direzioni:
- Post Quantum Cryptography (PQC);
- Quantum Key Distribution (QKD).
Entrambe le tecnologie verranno ampiamente discusse all’interno di questa rubrica, per ora ci si limita a darne un’intuizione sintetica. Con PQC si identifica la risposta della crittografia classica all’avvento del computer quantistico.
La PQC mira all’individuazione di schemi crittografici asimmetrici la cui sicurezza sia basata su problemi matematici considerati resistenti ad algoritmi quantistici e, di conseguenza, distinti da fattorizzazione e logaritmo discreto. In questo senso è in corso un processo di standardizzazione di nuovi algoritmi crittografici da parte del National Institute of Standards and Technology (NIST).
D’altra parte, la QKD è una tecnologia che sfrutta i principi della meccanica quantistica per realizzare uno scambio chiave a sicurezza incondizionata, basato sulle leggi della fisica e non sull’assunzione di intrattabilità computazionale di specifici problemi matematici.
Molti temi legati a questa tecnologia sono ancora oggetto di ricerca in ambito accademico e industriale, ciò nonostante sono già presenti sul mercato soluzioni di QKD caratterizzate da un TRL medio-alto.
Per continuare a garantire ai propri clienti elevati standard di sicurezza anche nella cosiddetta “Quantum Era”, l’impegno di Telsy si sta orientando su entrambe le soluzioni, da una parte grazie alle competenze crittografiche classiche, storicamente tratto distintivo dell’azienda, dall’altra con la recente entrata nel capitale di QTI, spin off del CNR di Firenze con specifiche competenze nel campo delle tecnologie quantistiche e dello scambio quantistico delle chiavi.
FONTI:
Immagine 2: https://www.pngarts.com/explore/289623
Immagine 3: https://optimization.mccormick.northwestern.edu/index.php/Traveling_salesman_problems
Questo articolo appartiene ad una serie di contributi, a cura del Gruppo di Ricerca in Crittografia di Telsy, dedicata al calcolo quantistico e alle sue implicazioni sulla Crittografia. Per la consultazione di altri articoli si rimanda all’indice della rubrica.
Per altri articoli relativi ai temi Quantum e Crittografia si rimanda alle relative categorie nel blog.
L’autore
Francesco Stocco, laureato magistrale in Matematica presso l’Università degli Studi di Padova e l’Université de Bordeaux frequentando il percorso di studi “Algebra Geometry And Number Theory” (ALGANT), entrato a far parte del gruppo di ricerca in Crittografia di Telsy alla fine del 2020 occupandosi in particolare di temi inerenti alle tecnologie quantistiche.
